原文链接:CHAPTER 1 Using neural nets to recognize handwritten digits
本书序言
在传统的编程方法中,我们告诉计算机做什么,把大问题分成许多小的、精确定义的任务,计算机可以很容易地执行。相比之下,在神经网络中,我们不告诉计算机如何解决我们的问题。相反,它从观测数据中学习,找出它自己的解决问题的方法。
一个以原理为导向的方法
本书一个坚定的信念,是让读者更好地去深刻理解神经网络和深度学习,而不是像一张冗长的洗衣单一样模糊地列出一堆想法。如果你很好理解了核心理念,你就可以很快地理解其他新的推论。用编程语言对比,把这理解为掌握一种新语言的核心语法、库和数据结构。你可能仍然只是``知道’’整个编程语言的一小部分—-许多编程语言有巨大的标准库—-但新的库和数据结构可以很快且容易被理解。
这就意味着这本书的重点不是作为一个如何使用一些特定神经网络库的教程。如果你主要想围绕着某个程序库的方式去学习,那不要读这本书!找到你想学习的程序库,并通过教程和文档来完成。注意这点。虽然这也许能很快解决你的问题,但是,如果你想理解神经网络中究竟发生了什么,如果你想要了解今后几年都不会过时的原理,那么只是学习些热门的程序库是不够的。你需要领悟让神经网络工作的原理。技术来来去去,但原理是永恒的。
一个动手实践的方法
我们将通过攻克一个具体的问题:教会计算机识别手写数字的问题,来学习神经网络和深度学习的核心理论。 这个问题用常规的方法来编程解决是非常困难的。然而,正如我们所看到的,它可以很好地利用一个简单的神经网络来解决,只需几十行代码,没有特别的库。更多的是,我们会通过多次迭代来改进程序,逐步融入神经网络和深度学习的核心思想。
难得有一本书能兼顾理论和动手实践。但是我相信,如果我们建立了神经网络的基本思路,你会学到最好的。我们将开发实际能用的代码,而不仅仅是抽象的理论,这些代码你可以探索和扩展。这样你就可以理解其基础,不论是理论还是实践,并且扩展和提高你的知识面。
使用神经网络识别手写数字——感知器
本章我们将实现一个可以识别手写数字的神经网络。这个程序仅仅 74 行,不使用特别的神经网络库。然而,这个短小的网络不需要人类帮助便可以超过 96% 的准确率识别数字。而且,在后面的章节,我们会发展出将准确率提升到 99% 的技术。实际上,最优的商业神经网络已经足够好到被银行和邮局分别用在账单核查和识别地址上了。
手写识别常常被当成学习神经网络的原型问题,因此我们聚焦在这个问题上。作为一个原型,它具备一个关键点:挑战性,识别手写数字并不轻松,但也不会难到需要超级复杂的解决方法,或者超大规模的计算资源。另外,这其实也是一种发展出诸如深度学习更加高级的技术的方法。所以,整本书我们都会持续地讨论手写数字识别问题。本书后面部分,我们会讨论这些想法如何用在其他计算机视觉的问题或者语音、自然语言处理和其他一些领域中。
当然,如果仅仅为了编写一个计算机程序来识别手写数字,本章的内容可以简短很多!但前进的道路上,我们将扩展出很多关于神经网络的关键的思想,其中包括两个重要的人工神经元感知机和 S 型神经元),以及标准的神经网络学习算法,即随机梯度下降算法。自始至终,我专注于解释事情的原委,并构筑你对神经网络的直观感受。这需要一个漫长的讨论,而不是仅仅介绍些基本的技巧,但这对于更深入的理解是值得的。作为收益,在本章的最后,我们会准备好了解什么是深度学习,以及它为什么很重要。
感知器
什么是神经网络?一开始,我将解释一种被称为“感知器”的人工神经元。今天,使用其它人工神经元模型更为普遍,在这本书中,以及更多现代的神经网络著作中,主要使用的是一种叫做 S 型的神经元模型。我们很快会讲到 S 型神经元。但是要理解为什么 S 型神经元被定义为那样的方式,值得花点时间先来理解下感知器。
感知器的定义
感知器是如何工作的呢?一个感知器接受几个二进制输入,$x_1,x_2,\ldots$,并产生一个二进制输出:
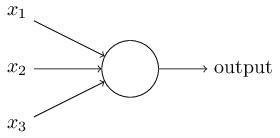
示例中的感知器有三个输入,$x_1,x_2,x_3$。通常可以有更多或更少输入。Rosenblatt 提议一个简单的规则来计算输出。他引入权重,$w_1,w_2,\ldots$,表示相应输入对于输出重要性的实数。神经元的输出,$0$ 或者 $1$,则由分配权重后的总和 $\sum_j w_j x_j$ 小于或者大于一些阈值决定。和权重一样,阈值是一个实数,一个神经元的参数。用更精确的代数形式:
这就是一个感知器所要做的所有事情!
目前为止我把像 $x_1$ 和 $x_2$ 这样的输入画成感知器网络左边浮动的变量。实际上,可以画一层额外的感知器输入层来方便对输入编码:
这种对有一个输出但没有输入的感知器的标记法,
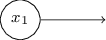
是一种标准。它并不实际表示一个感知器没有输入。为了看清它,假设我们确实有一个没有输入的感知器。那么加权和 $\sum_j w_j x_j$ 会总是为零,并且感知器在 $b > 0$ 时输出 $1$,当 $b \leq 0$时输出 $0$。那样,感知器会简单输出一个固定值,而不是期望值(上例中的 $x_1$)。倒不如完全不把输入感知器看作感知器,而是简单定义为输出期望值的特殊单元,$x_1, x_2,\ldots$。
感知器做决策的原理
随着权重和阈值的变化,你可以得到不同的决策模型。我们来看一个由感知器构成的网络。
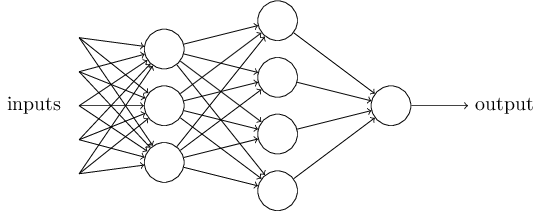
在这个网络中,第一列感知器我们称其为第一层感知器通过权衡输入依据做出三个非常简单的决定。那第二层的感知器呢?每一个都在权衡第一层的决策结果并做出决定。以这种方式,一个第二层中的感知器可以比第一层中的做出更复杂和抽象的决策。在第三层中的感知器甚至能进行更复杂的决策。以这种方式,一个多层的感知器网络可以从事复杂巧妙的决策。
顺便提一下,当我定义感知器时我说的是感知器只有一个输出。在上面的网络中感知器看上去像是有多个输出。实际上,他们仍然是单输出的。多个感知器输出箭头仅仅便于说明一个感知器的输出被用于其它感知器的输入。 它和把单个输出线条分叉相比,显得讨巧些。
让我们简化感知器的数学描述。条件 $\sum_j w_j x_j$ 看上去有些冗长,我们可以创建两个符号的变动来简化。第一个变动是把 $\sum_j w_j x_j$ 改写成点乘,$w\cdot x \equiv \sum_j w_j x_j$,这里 $w$ 和 $x$ 对应权重和输入的向量。第二个变动是把阈值移到不等式的另一边,并用感知器的偏置 $b \equiv -threshold$ 代替。用偏置而不是阈值,那么感知器的规则可以重写为
我们可以把偏置看作一种表示让感知器输出 $1$(或者用生物学的术语,即激活感知器)有多容易的估算。对于具有一个非常大偏置的感知器来说,输出 $1$ 是很容易的。但是如果偏置是一个非常小的负数,输出$1$ 则很困难。很明显,引入偏置只是我们描述感知器的一个很小的变动,但是我们后面会看到它引导更进一步的符号简化。因此,在这本书的后续部分,我们不再用阈值,而总是使用偏置。
感知器与逻辑运算
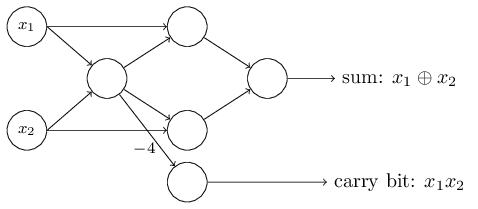
我已经描述过感知器是一种权衡依据来做出决策的方法。感知器被采用的另一种方式,是计算基本的逻辑功能,即我们通常认为的运算基础,例如“与”,“或”和“与非”。例如,假设我们有个两个输入的感知器,每个权重为 $-2$,整体的偏置为 $3$。这是我们的感知器,
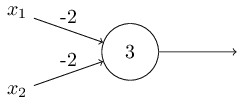
这样我们得到:输入00产生输出1,即 (-2)0 + (-2)0 + 3 = 3 是正数。这里我用符号来显式地表示乘法。但是输入11产生输出 0,即 (-2)1 + (-2)*1 + 3 = -1 是负数。如此我们的感知器实现了一个与非门!
与非门的例子显示了我们可以用感知器来计算简单的逻辑功能。实际上,我们完全能用感知器网络来计算任何逻辑功能。原因是与非门是通用运算,那样,我们能在多个与非门之上构建出任何运算。
感知器运算的通用性既是令人鼓舞的,又是令人失望的。令人鼓舞是因为它告诉我们感知器网络能和其它计算设备一样强大。但是它也令人失望,因为它看上去只不过是一种新的与非门。这简直不算个大新闻!
然而,实际情况比这一观点认为的更好。其结果是我们可以设计学习算法,能够自动调整人工神经元的权重和偏置。这种调整可以自动响应外部的刺激,而不需要一个程序员的直接干预。这些学习算法是我们能够以一种根本区别于传统逻辑门的方式使用人工神经元。有别于显式地设计与非门或其它门,我们的神经网络能简单地学会解决问题,这些问题有时候直接用传统的电路设计是很难解决的。
S 型神经元
学习算法听上去非常棒。但是我们怎样给一个神经网络设计这样的算法呢?假设我们有一个感知器网络,想要用它来解决一些问题。
引入 S 型神经元的原因
例如,网络的输入可以是一幅手写数字的扫描图像。我们想要网络能学习权重和偏置,这样网络的输出能正确分类这些数字。为了看清学习是怎样工作的,假设我们把网络中的权重(或者偏置)做些微小的改动。就像我们马上会看到的,这一属性会让学习变得可能。这里简要示意我们想要的(很明显这个网络对于手写识别还是太简单了!):
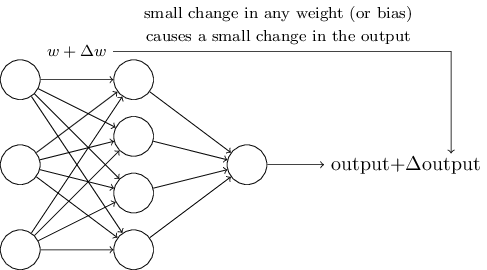
如果对权重(或者偏置)的微小的改动真的能够仅仅引起输出的微小变化,那我们可以利用这一事实来修改权重和偏置,让我们的网络能够表现得像我们想要的那样。例如,假设网络错误地把一个“9”的图像分类为“8”。我们能够计算出怎么对权重和偏置做些小的改动,这样网络能够接近于把图像分类为“9”。然后我们要重复这个工作,反复改动权重和偏置来产生更好的输出。这时网络就在学习。
问题是当我们给实际网络加上感知器时,结果并不像我们想象的那样。实际上,网络中单个感知器上一个权重或偏置的微小改动有时候会引起那个感知器的输出完全翻转,如 $0$ 变到 $1$。那样的翻转可能接下来引起其余网络的行为以极其复杂的方式完全改变。因此,虽然你的“9”可能被正确分类,网络在其它图像上的行为很可能以一些很难控制的方式被完全改变。这使得逐步修改权重和偏置来让网络接近期望行为变得困难。也许有其它聪明的方式来解决这个问题。但是目前为止,我们还没发现有什么办法能让感知器网络进行学习。
我们可以引入一种称为 S 型神经元的新的人工神经元来克服这个问题。S 型神经元和感知器类似,但是经过修改后,权重和偏置的微小改动只引起输出的微小变化。这对于让神经元网络学习起来是很关键的。
好了, 让我来描述下 S 型神经元。我们用描绘感知器的相同方式来描绘 S 型神经元:
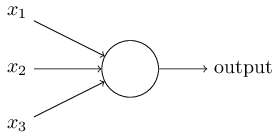
正如一个感知器, S 型神经元有多个输入,$x_1,x_2,\ldots$。但是这些输入可以取 $0$ 和$1$ 中的任意值,而不仅仅是 $0$ 或 $1$。例如,$0.638\ldots$ 是一个 S 型神经元的有效输入。同样, S 型神经元对每个输入有权重,$w_1,w_2,\ldots$,和一个总的偏置,$b$。但是输出不是 $0$ 或 $1$。相反,它现在是 $\sigma(w \cdot x+b)$,这里 $\sigma$ 被称为 S型函数(顺便提一下,$\sigma$ 有时被称为逻辑函数,而这种新的神经元类型被称为逻辑神经元。既然这些术语被很多从事于神经元网络的人使用,记住它是有用的。然而,我们将继续使用 S 型这个术语。)
定义为:
把它们放在一起来更清楚地说明,一个具有输入 $x_1,x_2,\ldots$,权重
$w_1,w_2,\ldots$,和偏置 $b$ 的 S 型神经元的输出是:
S 型神经元的性质
初看上去, S 型神经元和感知器有很大的差别。如果你不熟悉 S型函数的代数形式,它看上去晦涩难懂又令人生畏。实际上,感知器和 S 型神经元之间有很多相似的地方,跨过理解上的障碍,S 型神经元的代数形式具有很多技术细节。
为了理解和感知器模型的相似性,假设 $z \equiv w \cdot x + b$ 是一个很大的正数。那么 $e^{-z} \approx 0$ 而 $\sigma(z) \approx 1$。即,当 $z = w \cdot
x+b$ 很大并且为正, S 型神经元的输出近似为 $1$,正好和感知器一样。相反地,假设 $z = w \cdot x+b$ 是一个很大的负数。那么$e^{-z} \rightarrow \infty$,$\sigma(z) \approx 0$。所以当 $z = w \cdot x +b$ 是一个很大的负数, S 型神经元的行为也非常近似一个感知器。只有在 $w \cdot x+b$ 取中间值时,和感知器模型有比较大的偏离。
$\sigma$ 的代数形式又是什么?我们怎样去理解它呢?实际上,$\sigma$ 的精确形式不重要,重要的是这个函数绘制的形状。是这样:
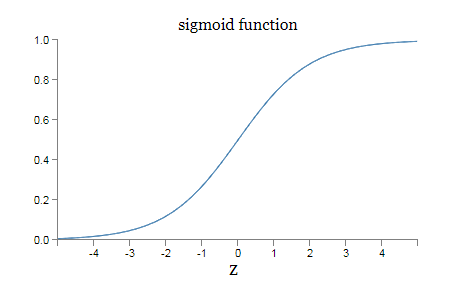
这个形状是阶跃函数平滑后的版本:
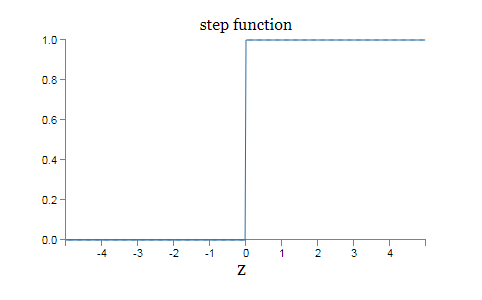
如果 $\sigma$ 实际是个阶跃函数,既然输出会依赖于 $w\cdot x+b$ 是正数还是负数。(实际上,当 $w \cdot x +b = 0$ ,感知器输出 $0$,而同时阶跃函数输出$1$。所以严格地说,我们需要修改阶跃函数来符合这点。但是你知道怎么做。)那么S型神经元会成为一个感知器。利用实际的 $\sigma$ 函数,我们得到一个,就像上面说明的,平滑的感知器。确实,$\sigma$ 函数的平滑特性,正是关键因素,而不是其细部形式。$\sigma$ 的平滑意味着权重和偏置的微小变化,即 $\Delta w_j$ 和 $\Delta b$,会从神经元产生一个微小的输出变化 $\Delta output$。实际上,微积分告诉我们 $\Delta output$ 可以很好地近似表示为:
其中求和是在所有权重 $w_j$ 上进行的,而 $\partial \, output /
\partial w_j$ 和$\partial \, output /\partial b$ 符号表示 $output$ 分别对于 $w_j$ 和 $b$ 的偏导数。如果偏导数这个概念让你不安,不必惊慌。上面全部用偏导数的表达式看上去很复杂,实际上它的意思非常简单(这可是个好消息):$\Delta output$ 是一个反映权重和偏置变化,即 $\Delta w_j$ 和$\Delta b$,的线性函数。利用这个线性特性,我们比较容易细微地修改权重和偏置的值,从而获得我们需要的细微的输出变化。所以,因为 S 型神经元具有与感知器类似的本质行为,它们可以帮助我们了解权重和偏置的变化如何影响输出值。
如果对 $\sigma$ 来说重要的是形状而不是精确的形式,那为什么要在公式$\sigma(z) \equiv \frac{1}{1+e^{-z}}$中给 $\sigma$ 使用特定的形式呢?事实上,在下文我们还将不时地考虑一些神经元,它们给其它激活函数 $f(\cdot)$ 输出是 $f(w \cdot x + b)$。当我们使用一个不同的激活函数,最大的变化是公式$\Delta output \approx \sum_j \frac{\partial \, output}{\partial w_j} \Delta w_j + \frac{\partial \, output}{\partial b} \Delta b$ 中用于偏导数的特定值的改变。事实证明当我们后面计算这些偏导数,用 $\sigma$ 会简化数学计算,这是因为指数在求导时有些可爱的属性。无论如何,$\sigma$ 在神经网络的工作中被普遍使用,并且是这本书中我们最常使用的激活函数。
S 型神经元与感知器的关系
一个感性的认识是:S 型神经元是阶跃函数平滑后的版本。
但可以在数学上证明如下两点:
假设我们把一个感知器网络中的所有权重和偏置乘以一个正的常数,$c>0$。可以证明网络的行为并没有改变。
假设我们有上题中相同的设置,一个感知器网络。同样假设所有输入被选中。我们不需要实际的输入值,仅仅需要固定这些输入。假设对于网络中任何特定感知器的输入 $x$, 权重和偏置遵循 $w \cdot x + b\neq 0$。现在用 S 型神经元替换所有网络中的感知器,并且把权重和偏置乘以一个正的常量 $c>0$。证明在 $c \rightarrow \infty$的极限情况下, S 型神经元网络的行为和感知器网络的完全一致。当一个感知器的 $w \cdot x + b = 0$ 时又为什么会不同?
解释 S 型神经元的输出
我们应该如何解释一个 S 型神经元的输出呢?很明显,感知器和 S 型神经元之间一个很大的不同是 S 型神经元不仅仅输出 $0$ 或 $1$。它可以输出 $0$ 到 $1$ 之间的任何实数,所以诸如 $0.173\ldots$ 和 $0.689\ldots$ 的值是合理的输出。这是非常有用的,例如,当我们想要输出来表示一个神经网络的图像像素输入的平均强度。但有时候这会是个麻烦。假设我们希望网络的输出表示“输入图像是一个9”或“输入图像不是一个9”。很明显,如果输出是 $0$ 或 $1$ 是最简单的,就像用感知器。但是在实践中,我们可以设定一个约定来解决这个问题,例如,约定任何至少为 $0.5$ 的输出为表示 “这是一个9”,而其它小于 $0.5$ 的输出为表示“不是一个9”。当我们正在使用这样的约定时,我总会清楚地提出来,这样就不会引起混淆。
人工神经元的其它模型
到现在,我们使用的神经元都是 S 型神经元。理论上讲,从这样类型的神经元构建起来的神经网络可以计算任何函数。实践中,使用其他模型的神经元有时候会超过 S 型网络。取决于不同的应用,基于其他类型的神经元的网络可能会学习得更快,更好地泛化到测试集上,或者可能两者都有。让我们给出一些其他的模型选择,便于了解常用的模型上的变化。
可能最简单的变种就是 tanh 神经元,使用双曲正切函数替换了 S 型函数。输入为 $x$,权重向量为 $w$,偏置为 $b$ 的 tanh 神经元的输出是
这其实和 S 型神经元关系相当密切。回想一下 $\tanh$ 函数的定义:
进行简单的代数运算,我们可以得到
也就是说,$\tanh$ 仅仅是 S 型函数的按比例变化版本。我们同样也能用图像看看 $\tanh$ 的形状:
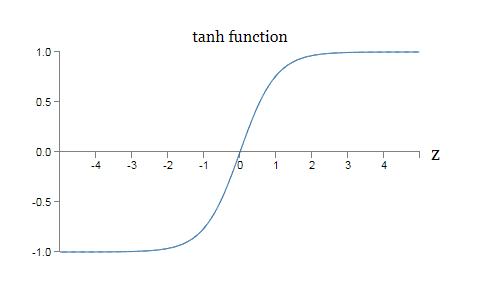
这两个函数之间的一个差异就是 $\tanh$ 神经元的输出的值域是 $(-1, 1)$ 而非 $(0,1)$。这意味着如果你构建基于 $\tanh$ 神经元,你可能需要正规化最终的输出(取决于应用的细节,还有你的输入),跟 sigmoid 网络略微不同。
类似于 S 型神经元,基于 S 型神经元的网络可以在理论上,计算任何将输入映射到$(-1, 1)$ 的函数(对于 tanh 和 S 型神经元,这个说法有一些技术上的预先声明。然而,非正式地,通常可以把神经网络看做可以以任意精度近似任何函数。)而且,诸如反向传播和随机梯度这样的想法也能够轻松地用在 tanh-neuron 神经元构成的网络上的。
参考文献
[1] Michael Nielsen. CHAPTER 1 Using neural nets to recognize handwritten digits[DB/OL]. http://neuralnetworksanddeeplearning.com/chap1.html, 2018-06-17.
[2] Zhu Xiaohu. Zhang Freeman.Another Chinese Translation of Neural Networks and Deep Learning[DB/OL]. https://github.com/zhanggyb/nndl/blob/master/chap1.tex, 2018-06-17.
[3] Michael Nielsen. CHAPTER 3 Improving the way neural networks learn[DB/OL]. http://neuralnetworksanddeeplearning.com/chap3.html, 2018-06-28.
[4] Zhu Xiaohu. Zhang Freeman.Another Chinese Translation of Neural Networks and Deep Learning[DB/OL]. https://github.com/zhanggyb/nndl/blob/master/chap3.tex, 2018-06-28.

