改进神经网络的学习方法——Softmax

原文链接：CHAPTER 3 Improving the way neural networks learn

Softmax 前言

我们大多数情况会使用交叉熵来解决学习缓慢的问题。但是，我希望简要介绍一下另一种解决这个问题的方法，基于 softmax 神经元层。在人工神经网络（ANN）中，softmax 通常被用作输出层的激活函数。这不仅是因为它的效果好，而且因为它使得 ANN 的输出值更易于理解。同时，softmax 配合 log 似然代价函数，其训练效果也要比采用二次代价函数的方式好。

Softmax 函数性质

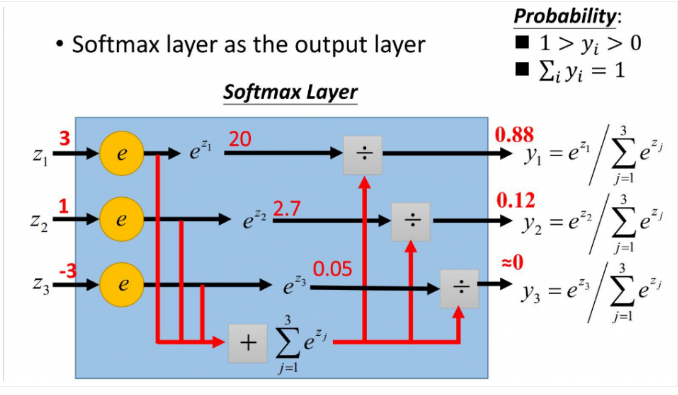
softmax的函数公式如下：

$$a^L_j = \frac{e^{z^L_j}}{\sum_k e^{z^L_k}},$$

在公式中的指数确保了所有的输出激活值是正数。然后方程中分母的求和又保证了 softmax 的输出和为 $1$。这个特定的形式确保输出激活值形成一个概率分布的自然的方式。你可以将其想象成一种重新调节 $z^L_j$ 的方法，然后将这个结果整合起来构成一个概率分布。

softmax函数最明显的特点在于：它把每个神经元的输入占当前层所有神经元输入之和的比值，当作该神经元的输出。这使得输出更容易被解释：神经元的输出值越大，则该神经元对应的类别是真实类别的可能性更高。

softmax 的单调性

证明如果 $j=k$ 则 $\partial a^L_j / \partial z^L_k$ 为正，$j \neq k$ 时为负。结果是，增加 $z^L_j$ 会提高对应的输出激活值 $a^L_j$ 并降低其他所有输出激活值。单调性证明见后文。

softmax的非局部性

softmax 层的一个好处是输出 $a^L_j$ 是对应带权输入 $a^L_j = \sigma(z^L_j)$ 的函数。由于分母求和所有的 $e^{z^L_k}$ 所以计算式子中计算每一个 $a_j^L$ 都与其他 $a_j^L$ 紧密相关。深入理解就是对于 softmax 层来说：任何特定的输出激活值 $a^L_j$ 依赖所有的带权输入。

逆转softmax层

假设我们有一个使用 softmax 输出层的神经网络，然后激活值 $a^L_j$ 已知。容易证明对应带权输入的形式为 $z^L_j = \ln a^L_j + C$，其中常量 $C$ 是独立于 $j$ 的。

Softmax 解决学习缓慢问题

我们现在已经对Softmax神经元层有了一定的认识。但是我们还没有看到一个Softmax层会怎么样解决学习缓慢问题。为了理解这点，让我们先定义一个对数似然函数。我们使用 $x$ 表示网络的训练输入，$y$ 表示对应的目标输出。然后关联这个训练输入的代价函数就是

$$C \equiv -\ln a^L_y$$

所以，如果我们训练的是 MNIST 图像，输入为 $7$ 的图像，那么对应的对数似然代价就是 $-\ln a_7^L$。看看这个直觉上的含义，想想当网络表现很好的时候，也就是确认输入为 $7$ 的时候。这时，他会估计一个对应的概率 $a_7^L$ 跟$1$ 非常接近，所以代价 $-\ln a_7^L$ 就会很小。反之，如果网络的表现糟糕时，概率$a_7^L$ 就变得很小，代价 $-\ln a_7^L$ 随之增大。所以对数似然代价函数也是满足我们期待的代价函数的条件的。

那关于学习缓慢问题呢？为了分析它，回想一下学习缓慢的关键就是量 $\partial C /
\partial w^L_{jk}$ 和 $\partial C / \partial b^L_j$ 的变化情况。这里我不会显式地给出详细的推导，但是通过一点代数运算你会得

$$\frac{\partial C}{\partial b^L_j} = a^L_j-y_j$$ $$\frac{\partial C}{\partial w^L_{jk}} = a^{L-1}_k (a^L_j-y_j)$$

证明见 矩阵形式的Softmax多分类模型

这些方程其实和我们前面对交叉熵得到的类似。而且，正如前面的分析，这些表达式确保我们不会遇到学习缓慢的问题。事实上，把一个具有对数似然代价的 softmax 输出层，看作与一个具有交叉熵代价的 S 型输出层非常相似，这是很有用的。

有了这样的相似性，你应该使用一个具有交叉熵代价的 S 型输出层，还是一个具有对数似然代价的Softmax输出层呢？实际上，在很多应用场景中，这两种方式的效果都不错。作为一种通用的视角，Softmax加上对数似然的组合更加适用于那些需要将输出激活值解释为概率的场景。那并不总是一个需要关注的问题，但是在诸如 MNIST 这种有着不重叠的分类问题上确实很有用。

数学形式证明 Softmax 有效性

softmax的函数公式如下：

$$a^L_j = \frac{e^{z^L_j}}{\sum_k e^{z^L_k}},$$

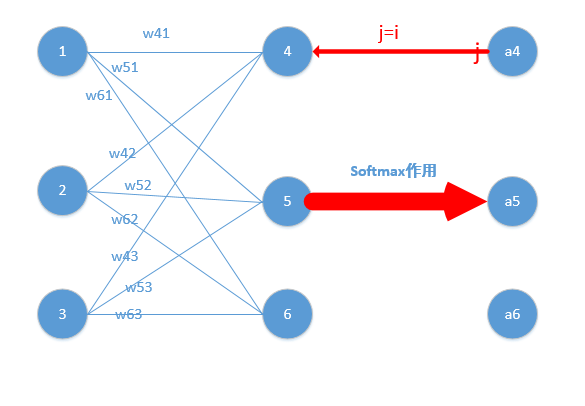
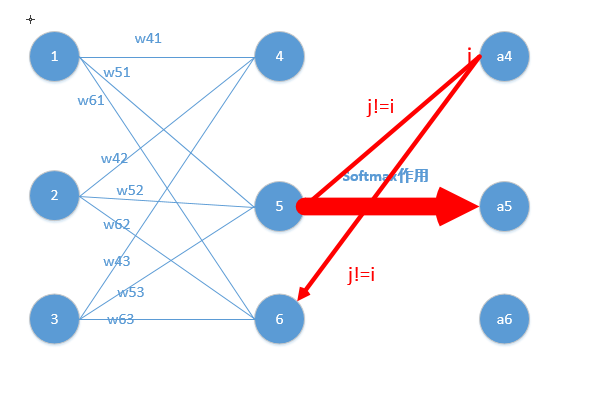
softmax在的求导结果比较特别，分为两种情况。

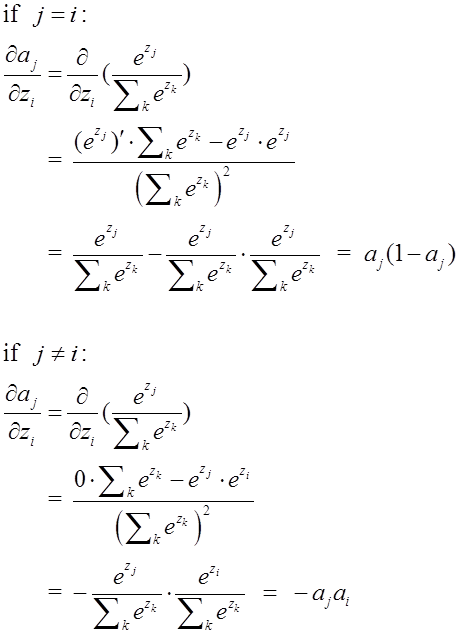
上文讲到，二次代价函数在训练ANN时可能会导致训练速度变慢的问题。那就是，初始的输出值离真实值越远，训练速度就越慢。这个问题可以通过采用交叉熵代价函数来解决。其实，这个问题也可以采用另外一种方法解决，那就是采用 softmax 激活函数，并采用log似然代价函数（log-likelihood cost function）来解决。

log似然代价函数的公式为：

$$C = - \sum_i y_i log a_i$$

注意这种情况：
其中，表示第 $a_k$ 个神经元的输出值，$y_k$ 表示第 k 个神经元对应的真实值，取值为 0 或 1 。由于 $y_k$ 取值为 0 或 1 ，对于每一个样本， $y_1,y_2,..,y_k$ 只会有一个取 1 其余的都取值为0， 所以对数似然函数求和符号可以去掉，化简为

$$C \equiv -\ln a^L_j$$

为了检验 softmax 和这个代价函数也可以解决上述所说的训练速度变慢问题，接下来的重点就是推导ANN的权重 w 和偏置 b 的梯度公式。

先求损失函数对偏置b的偏导数：

当 $i=j$ 时，带入 上面的结果$\frac{\partial a^L_j}{\partial z^L_i}=a_j^L(1-a_j^L)$

$$\begin{aligned} \frac{\partial C}{\partial b_{j}^L} &= \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_i} \\ &= - \frac{1}{a^L_j} [a_j^L(1-a_j^L)] \\ &= a_j^L -1 \end{aligned}$$

当 $i\not= j$ 时，带入 上面的结果$\frac{\partial a^L_j}{\partial z^L_i}=-a_j^La_i^L$

$$\begin{aligned} \frac{\partial C}{\partial b_{j}^L} &= \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_i} \\ &= - \frac{1}{a^L_j} (-a_j^La_i^L) \\ &= a_i^L \end{aligned}$$

根据反向传播的四个方程，具体分析见《反向传播算法》

可以知道，$\frac{\partial C}{\partial b^l_j} =\delta^l_j$ 和 $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$

所以,当 $i=j$ 时，

$$\frac{\partial C}{\partial w^L_{jk}} = a^{L-1}_k (a^L_j-1)$$

当 $i\not= j$ 时，

$$\frac{\partial C}{\partial w^L_{jk}} = a^{L-1}_k a_i$$

举个例子
通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],那么经过softmax函数作用后概率分别就是=[e^2/(e^2+e^3+e^4),e^3/(e^2+e^3+e^4),e^4/(e^2+e^3+e^4)] = [0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导（实际上这个偏导就是 $\delta^L$ 或者说是 $\partial C/\partial b^L$ ）就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！然后再根据这个进行back propagation就可以了

---

注意！当 $y_j$ 取值不为 0 或 1，而是区间 [0,1] 的一个实数值时，上面的式子只需稍稍做点修改，只需把下面式子中 $\frac{\partial C}{\partial a^L_j}$ 的结果从 $\frac{1}{a^L_j}$ 改为 $\frac{y_i}{a^L_j}$ 即可，

$$\begin{aligned} \frac{\partial C}{\partial b_{j}^L} &= \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_i} \\ &= - \frac{1}{a^L_j} [a_j^L(1-a_j^L)] \\ &= a_j^L -1 \end{aligned}$$

其它的求导过程也要做相应调整。所以在有的地方会看到这样的公式，

$$\frac{\partial C}{\partial b^L_j} = a^L_j-y_j$$ $$\frac{\partial C}{\partial w^L_{jk}} = a^{L-1}_k (a^L_j-y_j)$$

两者都是正确的，只是因为前提不一样，所以结论也有差异。

交叉熵与对数似然的关系

结论：交叉熵和最大似然的loss函数是一致的，在样本所属分类是唯一的情况下。

两者能够和谐统一的关键点是：

样本所属类别是唯一的，样本一定是某一类的，似然的思想是抽样样本的概率最大化，所以每一个样本只能处于一个固定的状态。这就使得每个样本的概率形式可以写成一个综合的形式，而综合的形式呢刚好可以在log下拆分成交叉熵的样子。在多类下，若样本所属类别是唯一的，最大似然的loss与交叉熵的loss仍然是一致的。

论证：

二项分布

二项分布也叫 0-1 分布，如随机变量 x 服从二项分布，关于参数 μ（0≤μ≤1），其值取 1 和取 0 的概率如下：

$$p(x=1|\mu)=\mu$$ $$p(x=0|\mu)=1-\mu$$

则在 x 上的概率分布为：

$$\text{Bern}(x|\mu)=\mu^x(1-\mu)^{1-x}$$

服从二项分布的样本集的对数似然函数

给定样本集 D={x1,x2,…,xB} 是对随机变量 x 的观测值，假定样本集从二项分布 p(x|μ) 中独立（p(x1,x2,…,xN)=∏ip(xi)）采样得来，则当前样本集关于 μ 的似然函数为：

$$p(\mathcal D|\mu)=\prod_{n=1}^Np(x_n|\mu)=\prod_{n=1}^N\mu^{x_n}\left(1-\mu\right)^{1-x_n}$$

从频率学派的观点来说，通过最大似然函数的取值，可以估计参数 μ，最大化似然函数，等价于最大化其对数形式：

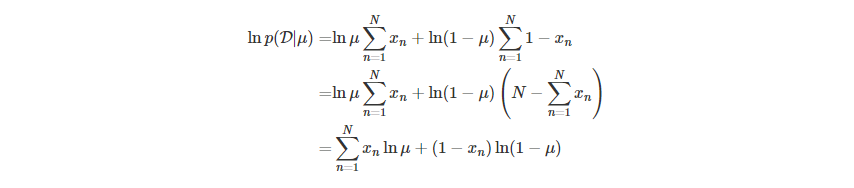
求其关于 μ 的导数，解得 μ 的最大似然解为：

$$\mu_{ML}=\frac1N\sum_{n=1}^Nx_n$$

这里我们仅关注：

$$\ln P(\mathcal D|\mu)=\sum_{n=1}^Nx_n\ln \mu+(1-x_n)\ln(1-\mu)$$

交叉熵损失函数

$$L_H(\mathbf x,\mathbf z)=-\sum_{n=1}^Nx_n\log z_n+(1-x_n)\log(1-z_n)$$

x 表示原始信号，z 表示重构信号。（损失函数的目标是最小化，似然函数则是最大化，二者仅相差一个符号）。

---

参考文献

[1] Michael Nielsen.CHAPTER 3 Improving the way neural networks learn[DB/OL]. http://neuralnetworksanddeeplearning.com/chap3.html, 2018-06-22.

[2] Zhu Xiaohu. Zhang Freeman.Another Chinese Translation of Neural Networks and Deep Learning[DB/OL].https://github.com/zhanggyb/nndl/blob/master/chap3.tex, 2018-06-22.

[3] __鸿. softmax的log似然代价函数（公式求导）[DB/OL]. https://blog.csdn.net/u014313009/article/details/51045303. 2018-06-22.

[4] 忆臻HIT_NLP. 手打例子一步一步带你看懂softmax函数以及相关求导过程[DB/OL]. https://www.jianshu.com/p/ffa51250ba2e. 2018-06-22.