0%

变分自编码器（Variational Auto-Encoder，VAE）

发表于 更新于 分类于 ，

为什么要发明变分自编码器

什么是变分自编码机？

要理解变分自编码机(VAE)，我们要先从一个简单的网络开始，一步一步添加部件。

描述神经网络的常见方法，是把它解释成我们想要建模的功能的某种近似。然而，它们还能被理解为储存信息的某种数据结构。

假设有一个由数层解卷积层构成的神经网络，我们把输入设定为单位向量，然后训练该网络去降低其与目标图像之间的均方误差。这样，该图像的“数据”就包含在神经网络当前的参数之中了。

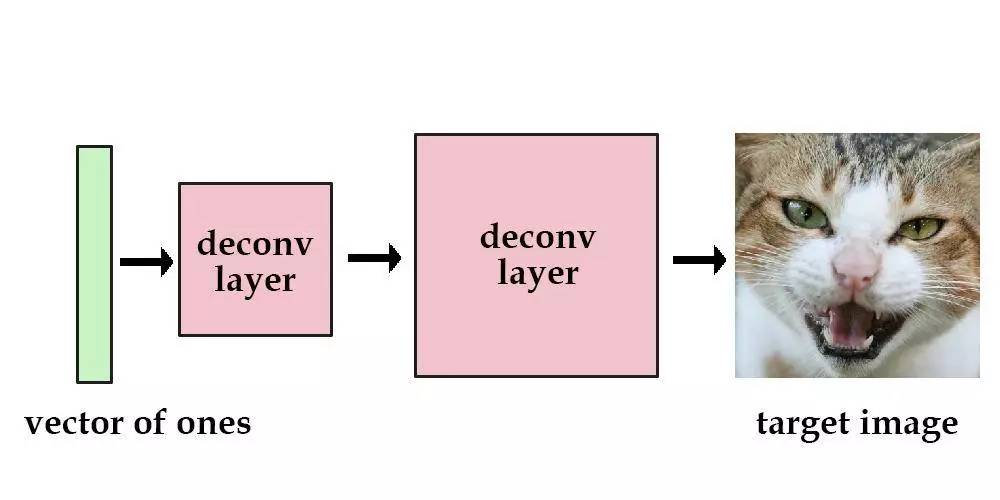
现在，我们用多张图像来尝试这一步骤。此时，输入不再是单位向量，而要改用独热向量。比如，输入 [1, 0, 0, 0] 可能是生成一张猫的图像，而输入 [0, 1, 0, 0] 则可能生成一张狗的图像。这是可行的，不过这样我们只能存储最多4张图像。让网络记住更多的图像则要使用更长的向量，同时也意味着越来越多的参数。

为此，我们需要使用实向量，而非独热向量。我们可以把它视为某个图像所对应的编码，比如用向量 [3.3, 4.5, 2.1, 9.8] 来表示猫的图像，而用向量 [3.4, 2.1, 6.7, 4.2] 来表示狗的图像，这就是 编码/解码 这一术语的来源。这一初始向量便是我们的潜在变量。

像我前面那样随机选择潜在变量，明显是个糟糕的做法。在自编码机中，我们加入了一个能自动把原始图像编码成向量的组件。上述解卷积层则能把这些向量“解码”回原始图像。

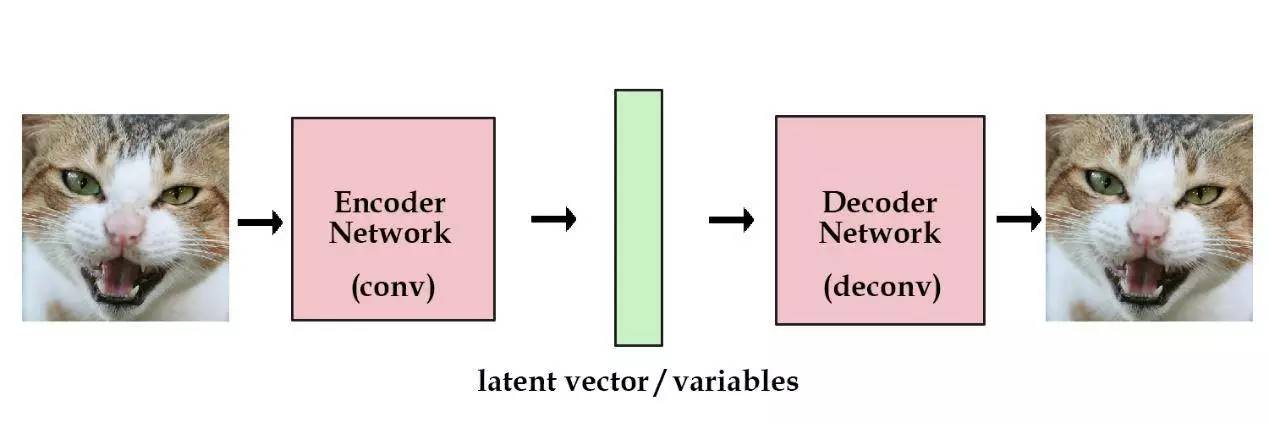
这样，我们的模型终于到了一个能有用武之地的阶段。根据需要，我们可以用尽可能多的图像来训练网络。如果保存了某张图像的编码向量，我们随时就能用解码组件来重建该图像，整个过程仅需一个标准的自编码机。

不过，这里我们想要的是构建一个生成式模型，而非仅仅是“记忆”图像数据的模糊结构。除了像前面那样从已有图像中编码出潜在向量，我们还不知道如何创造这些向量，也就无法凭空生成任何图像。

这里有个简单的办法。我们给编码网络增加一个约束，迫使它所生成的潜在向量大体上服从于单位高斯分布。该约束条件使得变分自编码机不同于标准自编码机。

现在，生成新的图像就变得容易了：我们只需从单位高斯分布中采样出一个潜在向量，并将其传到解码器即可。

实际操作中，我们需要仔细权衡网络的精确度与潜在变量在单位高斯分布上的契合程度。

神经网络可以自行决定这里的取舍。对于其中的误差项，我们归纳出独立的两种：生成误差，用以衡量网络重构图像精确度的均方误差；潜在误差，用以衡量潜在变量在单位高斯分布上的契合程度的KL散度。

generation_loss = mean(square(generated_image - real_image))

latent_loss = KL-Divergence(latent_variable, unit_gaussian)

loss = generation_loss + latent_loss

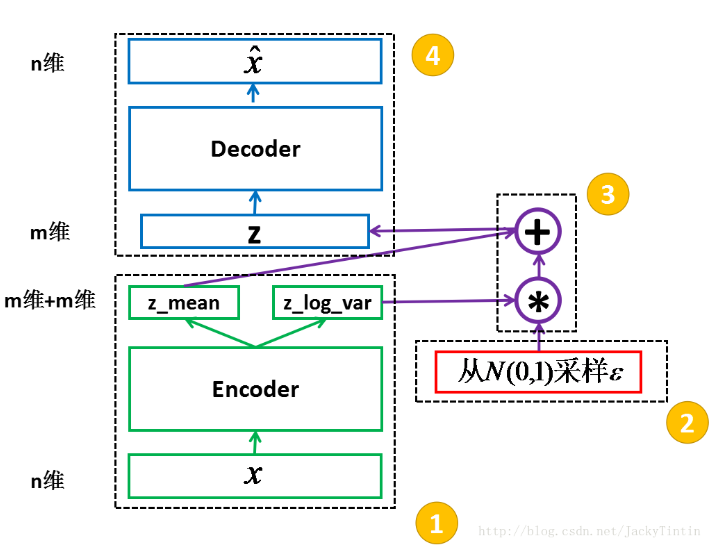
为了优化KL散度，我们要用到重新参数化的一个简单技巧：生成一个均值向量一个标准差向量，而非直接生成实值向量。

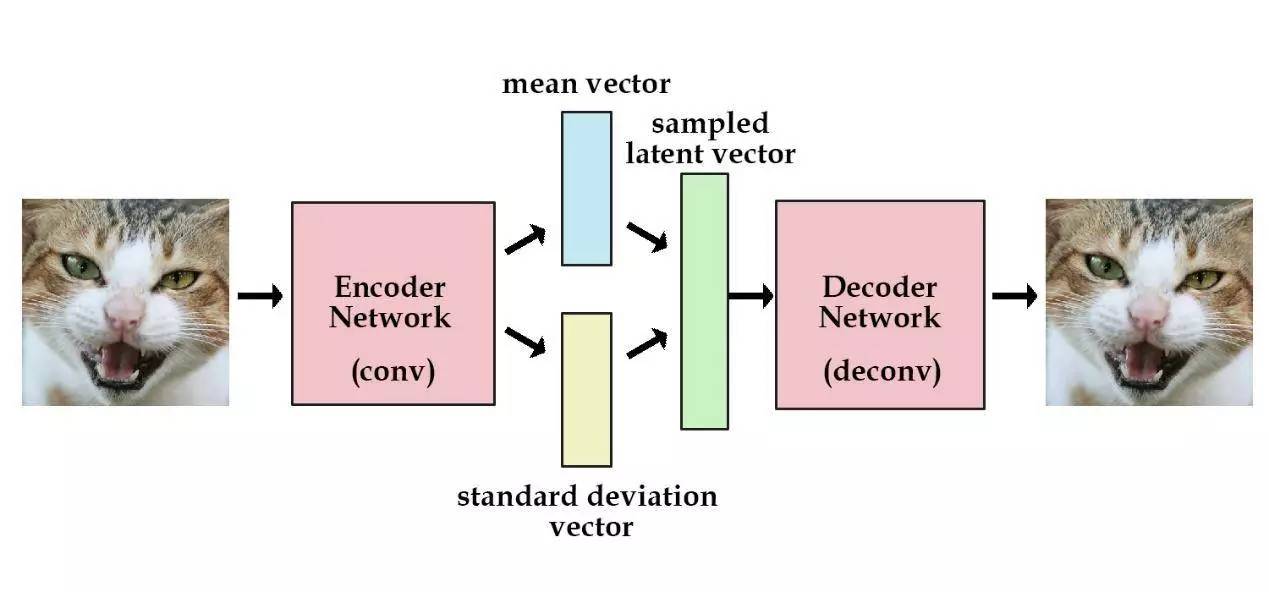
我们的KL散度计算就变成这样：

# z_mean and z_stddev are two vectors generated by encoder network

latent_loss = 0.5 * tf.reduce_sum(tf.square(z_mean) + tf.square(z_stddev) - tf.log(tf.square(z_stddev)) - 1,1)

在计算解码网络的误差时，我们只需从标准差中取样，再加上均值向量，就能得到我们的潜在向量：

samples = tf.random_normal([batchsize,n_z],0,1,dtype=tf.float32)

sampled_z = z_mean + (z_stddev * samples)

除了能让我们生成随机的潜在变量，该约束还能提高VAE网络的泛化能力。

形象地说，我们可以把潜在变量视为数据的变换系数。

在[ 0, 10 ]的区间内，假定你有一系列的实数-名称对，一个实数代表一个物体的名字。例如，5.43表示苹果，5.44表示香蕉。当有人给你数字5.43时，你肯定知道他们是在谈论苹果。本质上，采用这一方式可以编码无限多的信息，毕竟[ 0, 10 ]之间的实数是有无数个。

然而，如果每当有人给告诉你一个新数字，它的高斯噪点也会增加一个时，情况会变成怎样？比如说，你收到数字是5.43，其原始数值则应在[4.4 ~ 6.4]之间，那其他人所说的真实数字就有可能是5.44（香蕉）。

所增噪点的标准差越大，其均值变量所能传递的信息就越少。

用此相同的逻辑，我们就能在编码器和解码器之间传递潜在变量。对原始图像的编码越有效，我们在高斯分布上所能取样的标准差就越大，直至为1（标准正态分布）。

这一约束迫使编码器变得非常高效，从而能创造出信息丰富的潜在变量。它所提升的泛化能力，让我们随机生成或从非训练图像编码而来的潜在变量，在解码时将能产生更好的结果。

VAE的效果有多好？

我在MNIST手写数据集上做了一些测试，从中可以看出变分自编码机的效果有多好。

左：第1世代，中：第9世代，右：原始图像

看起来很不错！在我那没有显卡的笔记本上运行15分钟后，它就生成了一些很好的MNIST结果。

VAE的优点：

由于它们所遵循的是一种 编码-解码 模式，我们能直接把生成的图像同原始图像进行对比，这在使用GAN时是不可能的。

VAE的不足：

由于它是直接采用均方误差而非对抗网络，其神经网络倾向于生成更为模糊的图像。

也有一些需要结合VAE和GAN的研究工作：采用相同的 编码器-解码器 配置，但使用对抗网络来训练解码器。

研究详情参考论文

https://arxiv.org/pdf/1512.09300.pdf

http://blog.otoro.net/2016/04/01/generating\-large\-images\-from\-latent\-vectors/

变分自编码器经典论文


《Auto-Encoding Variational Bayes》 | Diederik P Kingma, Max Welling | 2013

Abstract
如何在有向概率模型中进行有效的推理和学习，在存在连续的潜在变量和难以处理的后验分布和大数据集的情况下？我们引入一个随机变分推理和学习算法，缩放到大数据集，并在一些温和的可微性条件下，甚至在棘手的情况下工作。我们的贡献是双重的。首先，我们表明，变分下界的重新参数化产生一个下界估计，可以直接使用标准随机梯度方法优化。第二，我们表明，对于I.I.D.数据集具有连续潜变量每个数据点，后推理可以特别有效的拟合近似推理模型（也称为识别模型）棘手的后部使用所提出的下界估计。理论优势反映在实验结果中。
Subjects: Machine Learning (stat.ML); Machine Learning (cs.LG)

变分自编码器导论

变分自编码器基础

首先阅读苏剑林 VAE 的第一篇文章《变分自编码器（一）：原来是这么一回事》。

下面示意 VAE 代码完整版 。

VAE 的示意图

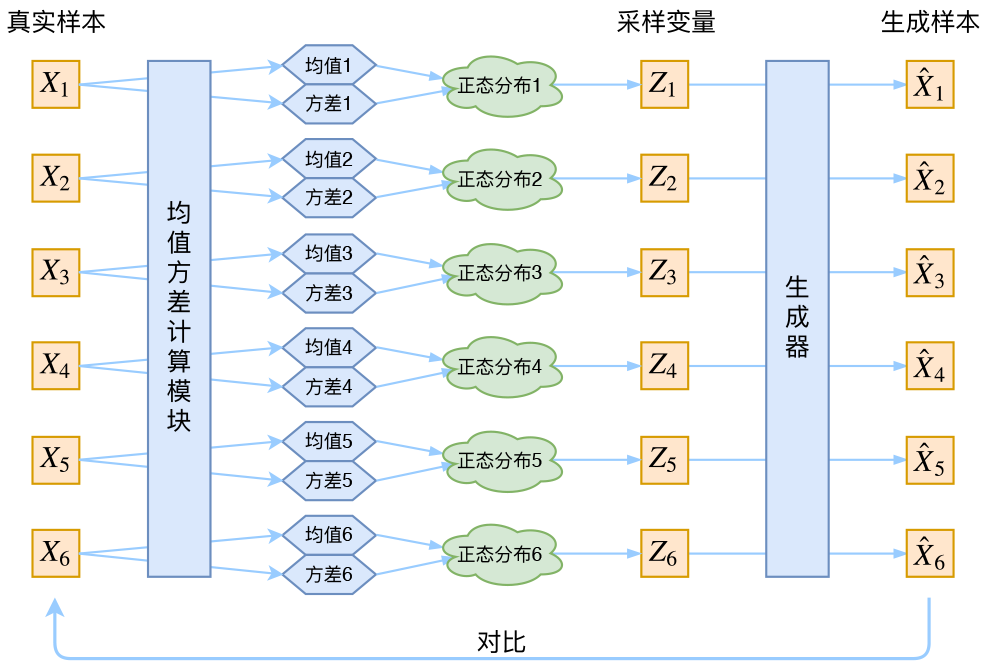
VAE由三部分组成：编码器 $q(z|x)$，先验 $p(z)$，解码器 $p(x|z)$。

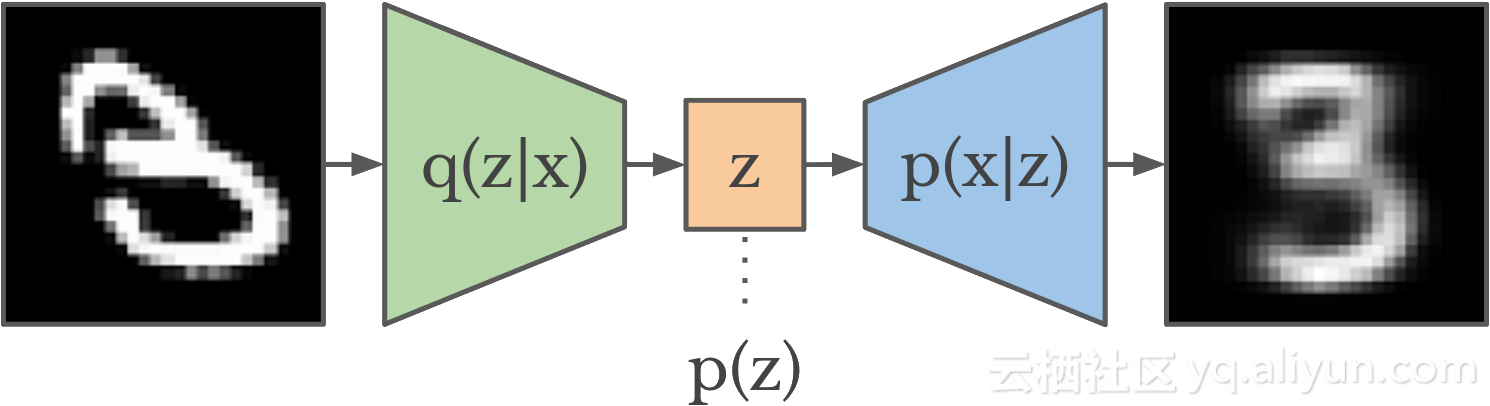
编码器将图像映射到针对该图像的代码的分布上。这种分布也被称为后验（posterior），因为它反映了我们关于代码应该用于给定图像之后的准确度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
'''Example of VAE on MNIST dataset using MLP

The VAE has a modular design. The encoder, decoder and VAE
are 3 models that share weights. After training the VAE model,
the encoder can be used to  generate latent vectors.
The decoder can be used to generate MNIST digits by sampling the
latent vector from a Gaussian distribution with mean=0 and std=1.

# Reference

[1] Kingma, Diederik P., and Max Welling.
"Auto-encoding variational bayes."
https://arxiv.org/abs/1312.6114
'''

VAE 网络结构

1
2
3
4
5
6
7
# network parameters
input_shape = (original_dim, )
intermediate_dim = 512
batch_size = 128
latent_dim = 2 #可以是其它维度，这里选择二维只是为了方便可视化
epochs = 50
# VAE model = encoder + decoder

编码器


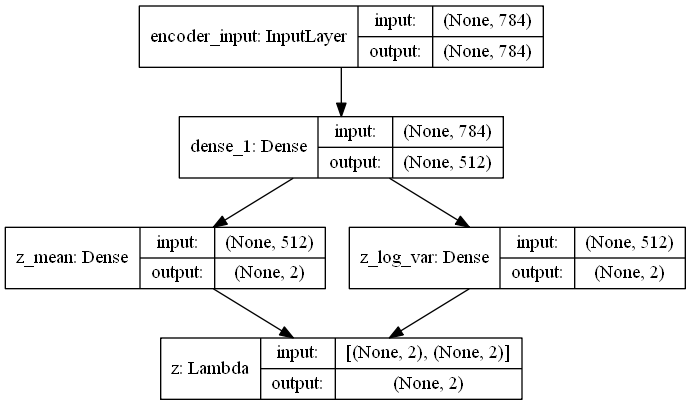
1
2
3
4
5
6
7
8
9
10
11
12
# build encoder model
inputs = Input(shape=input_shape, name='encoder_input')
x = Dense(intermediate_dim, activation='relu')(inputs)
z_mean = Dense(latent_dim, name='z_mean')(x)
z_log_var = Dense(latent_dim, name='z_log_var')(x)

# use reparameterization trick to push the sampling out as input
# note that "output_shape" isn't necessary with the TensorFlow backend
z = Lambda(sampling, output_shape=(latent_dim,), name='z')([z_mean, z_log_var])

# instantiate encoder model
encoder = Model(inputs, [z_mean, z_log_var, z], name='encoder')

解码器


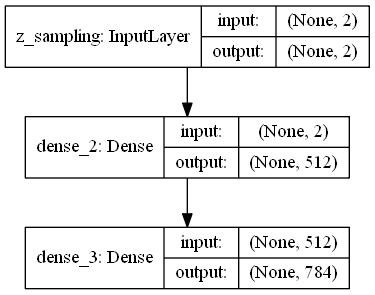
1
2
3
4
5
6
7
# build decoder model
latent_inputs = Input(shape=(latent_dim,), name='z_sampling')
x = Dense(intermediate_dim, activation='relu')(latent_inputs)
outputs = Dense(original_dim, activation='sigmoid')(x)

# instantiate decoder model
decoder = Model(latent_inputs, outputs, name='decoder')

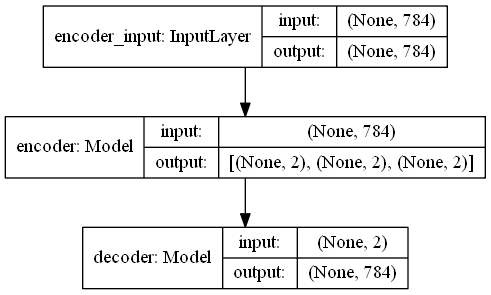
VAE


1
2
3
# instantiate VAE model
outputs = decoder(encoder(inputs)[2]) #前两维度分别是均值和“方差”
vae = Model(inputs, outputs, name='vae_mlp')

重参数技巧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# reparameterization trick
# instead of sampling from Q(z|X), sample eps = N(0,I)
# z = z_mean + sqrt(var)*eps
def sampling(args):
    """Reparameterization trick by sampling fr an isotropic unit Gaussian.

    # Arguments:
        args (tensor): mean and log of variance of Q(z|X)

    # Returns:
        z (tensor): sampled latent vector
    """

    z_mean, z_log_var = args
    # K is the keras backend
    batch = K.shape(z_mean)[0]
    dim = K.int_shape(z_mean)[1]
    # by default, random_normal has mean=0 and std=1.0
    epsilon = K.random_normal(shape=(batch, dim))
    return z_mean + K.exp(0.5 * z_log_var) * epsilon

VAE 本质结构

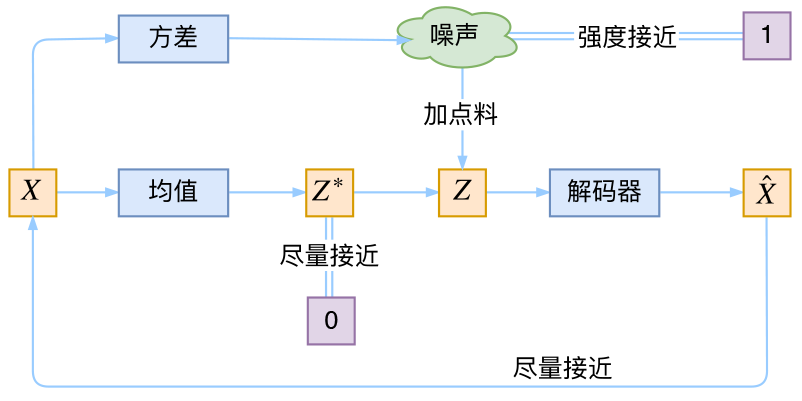
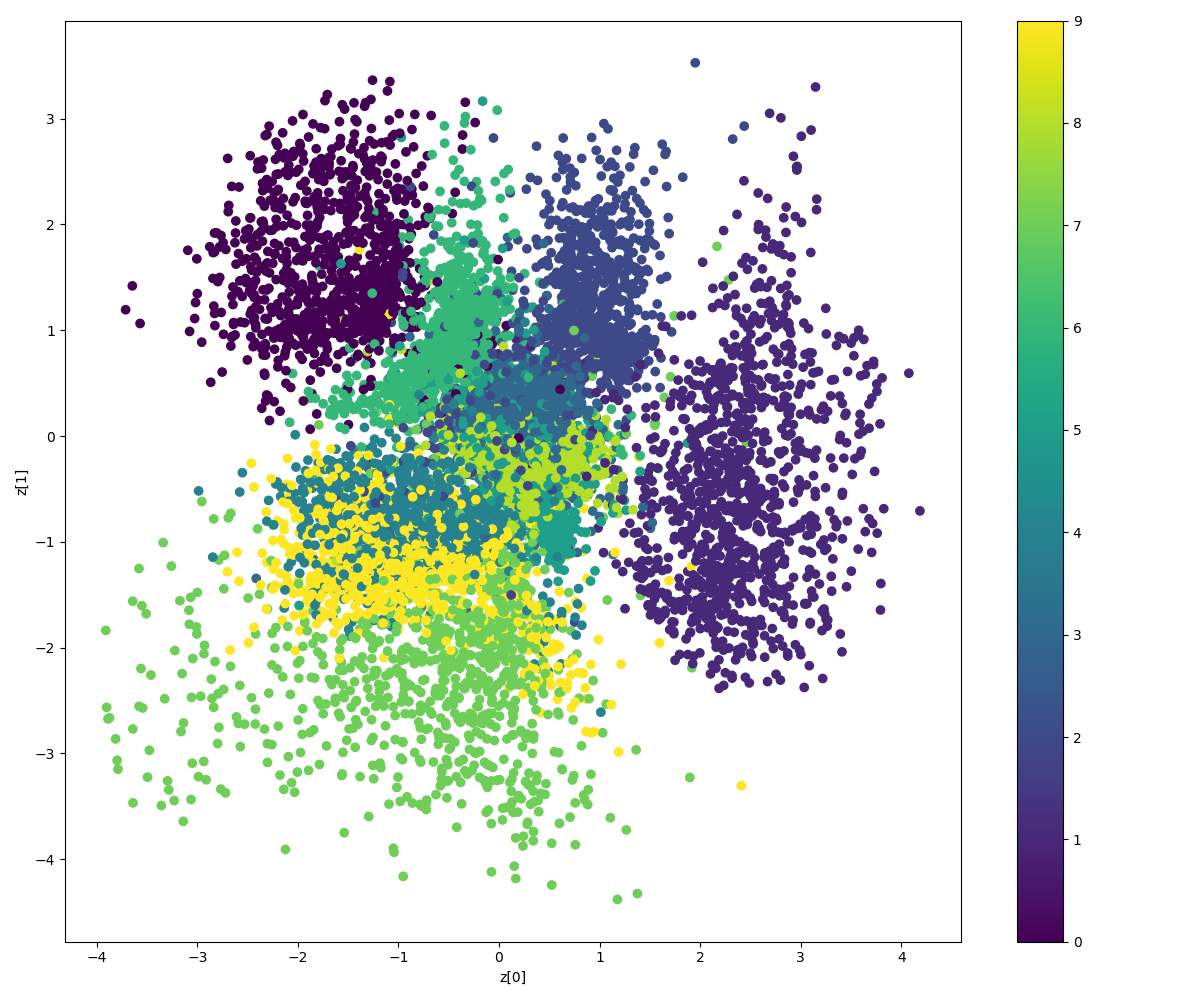
网络输出结果

网络输入时 MNIST 数据集

1
2
3
4
5
6
7
8
9
# MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()

image_size = x_train.shape[1]
original_dim = image_size * image_size
x_train = np.reshape(x_train, [-1, original_dim])
x_test = np.reshape(x_test, [-1, original_dim])
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255


继续深入研究 VAE

《变分自编码器（二）：从贝叶斯观点出发》
《变分自编码器（三）：这样做为什么能成？》
《what-is-variational-autoencoder-vae-tutorial》

条件变分自编码器

Conditional Variational Autoencoders | Isaac Dykeman

TODO：Variational AutoEncoder系列

参考文献

[1] 苏剑林‏. 变分自编码器（一）：原来是这么一回事[DB/OL]. https://spaces.ac.cn/archives/5253, 2018-08-14.

[2] 苏剑林‏. 变分自编码器（二）：从贝叶斯观点出发[DB/OL]. https://spaces.ac.cn/archives/5343, 2018-08-15.

[3] 苏剑林‏. 变分自编码器（三）：这样做为什么能成？[DB/OL]. https://spaces.ac.cn/archives/5383, 2018-08-15.

[4] Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. 2013.

[5] Isaac Dykeman‏. Conditional Variational Autoencoders[DB/OL]. http://ijdykeman.github.io/ml/2016/12/21/cvae.html, 2018-08-15.

[6] MoussaTintin. Learning Notes】变分自编码器（Variational Auto-Encoder，VAE）[DB/OL]. https://blog.csdn.net/JackyTintin/article/details/53641885, 2018-08-15.

[7] AI科技大本营. 什么！你竟然还不懂变分自编码机？这个16岁的OpenAI天才实习生讲得可透彻了[DB/OL]. https://www.sohu.com/a/162863895_697750, 2018-08-26.

本站所有文章和源码均免费开放，如您喜欢，可以请我喝杯咖啡