什么是赋范线性空间、内积空间,度量空间,希尔伯特空间 ?
qang pan 的解释
现代数学的一个特点就是以集合为研究对象,这样的好处就是可以将很多不同问题的本质抽象出来,变成同一个问题,当然这样的坏处就是描述起来比较抽象,很多人就难以理解了。既然是研究集合,每个人感兴趣的角度不同,研究的方向也就不同。为了能有效地研究集合,必须给集合赋予一些“结构”(从一些具体问题抽象出来的结构)。从数学的本质来看,最基本的集合有两类:线性空间(有线性结构的集合)、度量空间(有度量结构的集合)。对线性空间而言,主要研究集合的描述,直观地说就是如何清楚地告诉地别人这个集合是什么样子。为了描述清楚,就引入了基(相当于三维空间中的坐标系)的概念,所以对于一个线性空间来说,只要知道其基即可,集合中的元素只要知道其在给定基下的坐标即可。但线性空间中的元素没有“长度”(相当于三维空间中线段的长度),为了量化线性空间中的元素,所以又在线性空间引入特殊的“长度”,即范数。赋予了范数的线性空间即称为赋犯线性空间。但赋范线性空间中两个元素之间没有角度的概念,为了解决该问题,所以在线性空间中又引入了内积的概念。因为有度量,所以可以在度量空间、赋范线性空间以及内积空间中引入极限,但抽象空间中的极限与实数上的极限有一个很大的不同就是,极限点可能不在原来给定的集合中,所以又引入了完备的概念,完备的内积空间就称为Hilbert空间。这几个空间之间的关系是:线性空间与度量空间是两个不同的概念,没有交集。赋范线性空间就是赋予了范数的线性空间,也是度量空间(具有线性结构的度量空间)内积空间是赋范线性空间希尔伯特空间就是完备的内积空间。
TimXP 的解释
我们一般接触的是线性空间(向量空间) ,首先看线性空间和各种空间之间的关系:
- Linear Space 线性空间(向量空间)。线性空间又称作向量空间,关注的是向量的位置,对于一个线性空间,知道基(相当于三维空间中的坐标系)便可确定空间中元素的坐标(即位置);线性空间只定义了加法和数乘运算。如果我们想知道向量的长度怎么办?—-定义范数,引入赋范线性空间
- Normed Linear Space 赋范线性空间定义了范数的线性空间!如果我们想知道向量的夹角怎么办?—-定义内积,引入内积空间
- Inner Product Space 内积空间定义了内积的线性空间!
- Euclid Space 欧式空间定义了内积的有限维实线性空间!!如果我们想研究收敛性(极限)怎么办?—-定义完备
- Banach Space 巴纳赫空间,完备的赋范线性空间!
- Hilbert Space 希尔伯特空间完备的内积空间!(极限运算中不能跑出度量的范围)
他们之间的关系可以用下图表示: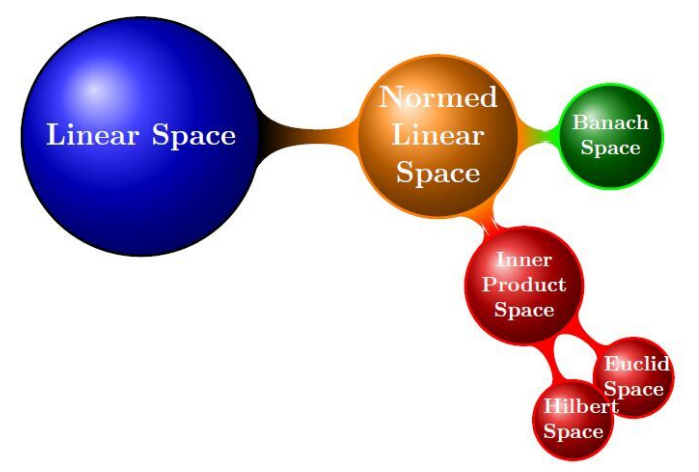
| 相关资料 | 说明 |
|---|---|
| 如何理解希尔伯特空间? | 知乎问答 |

