理解张量

神经网络的输入、输出、权重都是张量，神经网络中的各种计算和变换就是对张量操作，张量这种数据结构是神经网络的基石，可以说没有理解张量就没有真正理解神经网络和人工智能。本文由浅入深地详细讲解分析张量，望能给予读者启发——袁宵。

背景知识

连续值、有序值和分类值
在尝试理解数据时，应注意三种数值。

第一种是连续值。当以数字表示时，这些值是最直观的。它们是严格排序的，各个值之间的差异具有严格的含义。说明包装A比包装B重2公斤，或者包装B比包装A远100英里，这是有固定含义的，无论包装A重3公斤还是10公斤，或者包装B是从200英里还是2,000公斤。如果您要以单位进行计数或测量，则该值可能是连续值。
接下来是有序值。连续值的严格排序仍然保留，但是值之间的固定关系不再适用。一个很好的例子是订购小，中或大型饮料，将小号映射为值1，将中号映射为2，将大号映射为3。大号饮料大于中号，相同的方式是3大于2。但它并没有告诉您有关尺寸的任何信息。如果要将1、2和3转换为实际体积（例如8、12和24液体盎司），则这些值将切换为间隔值。重要的是要记住，除了对值进行排序外，您无法对它们进行数学运算；尝试平均大= 3和小= 1不会导致喝中杯！
最后，分类值既没有顺序也没有数字含义。这些值通常是可能性的枚举，并分配有任意数字。将水分配给1，将咖啡分配给2，将苏打分配给3，将牛奶分配给4是一个很好的例子。首先放水，最后放牛奶没有逻辑。您只需要不同的值就可以区分它们。您可以将咖啡分配给10，将牛奶分配给–3，而没有明显变化（尽管分配值的范围是0..N-1在稍后讨论一键编码时会很有优势）。

总结：连续值严格排序，各个值之间的差异具有严格的含义，可以进行数学运算；有序值严格排序，不可以进行数学运算；分类值仅有逻辑上的区别，排序和数学运算都没有意义。

张量的定义

张量（tensor）是一个多维数组（multidimensional arrays），即一种存储数字集合的数据结构，这些数字可通过索引（index）单独访问，并可通过多个索引进行索引。

张量是将向量和矩阵推广到任意维数。如下图所示，一个张量的维数与张量中用来表示标量值的索引的数量一致。

$$张量示意图$$

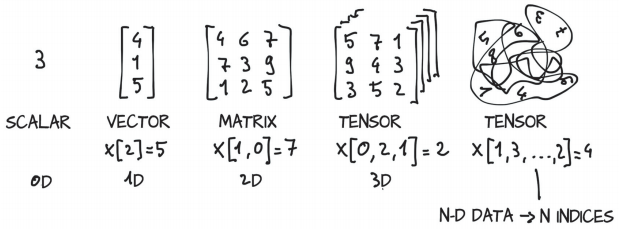
新张量 = 张量[索引]

张量的视图与存储

结合该文件理解以下内容：张量的存储.ipynb ，下面是该文件的主要内容：

• 张量，PyTorch中的基本数据结构
• 索引并在PyTorch张量上进行操作以探索和处理数据
• 与NumPy多维数组互操作
• 将计算移至GPU以提高速度

张量的视图与存储的定义

存储（Storage）是一维的数字数据数组，例如包含给定类型的数字(可能是float或int32)的连续内存块。张量是这样一个存储的视图，它能够通过使用偏移量（offset）和每一维度的步长（per-dimension strides）索引（index）到该存储中。存储的布局总是一维的，而与可能涉及到它的任何张量的维数无关。

多个张量可以对相同的存储进行索引，即使它们对数据的索引是不同的。但是，底层内存只分配一次，因此不管存储实例管理的数据有多大，都可以快速地创建数据上的替代张量视图。

$$张量是存储实例上的视图$$

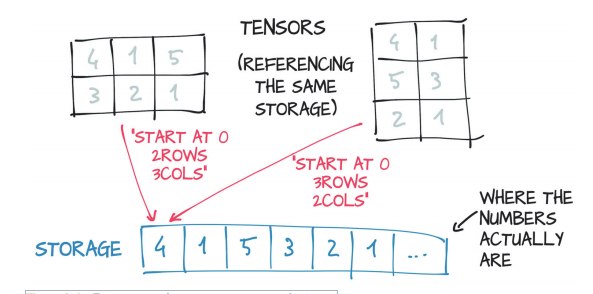
张量视图的多维性意义

张量的视图就是我们理解张量的方式，比如 shape 为[2,4,4,3]的张量 A，我们从逻辑上可以理解 为 2 张图片，每张图片 4 行 4 列，每个位置有 RGB 3 个通道的数据；张量的存储体现在张 量在内存上保存为一段连续的内存区域，对于同样的存储，我们可以有不同的理解方式， 比如上述 A，我们可以在不改变张量的存储下，将张量 A 理解为 2 个样本，每个样本的特征为长度 48 的向量。

张量存储的一维性

在存储数据时，内存并不支持这个维度层级概念，只能以平铺方式按序写入内存，因此这 种层级关系需要人为管理，也就是说，每个张量的存储顺序需要人为跟踪。为了方便表达，我们把张量 shape 中相对靠左侧的维度叫做大维度，shape 中相对靠右侧的维度叫做小维度，比如[2,4,4,3]的张量中，图片数量维度与通道数量相比，图片数量叫做大维度，通道 数叫做小维度。在优先写入小维度的设定下，形状（2, 3）张量的内存布局为：

<Tensor: shape=(3, 2), dtype=float32, numpy=
array([[1., 4.],
       [2., 1.],
       [3., 5.]], dtype=float32)>

[1., 4., 2., 1., 3., 5.]

数据在创建时按着初始的维度顺序写入，改变张量的视图仅仅是改变了张量的理解方 式，并不会改变张量的存储顺序，这在一定程度上是从计算效率考虑的，大量数据的写入 操作会消耗较多的计算资源。

张量存储的形状（大小）、存储偏移量和步长

为了索引到存储中，张量依赖于一些信息，这些信息连同它们的存储一起明确地定义了它们：大小、存储偏移量和步长（下图）。

中文	英文	意义
形状	shape	是一个元组，表示张量表示的每个维度上有多少个元素。注意张量的形状（shape）与存储的大小（size）等价。
步长	stride	是一个元组，表示当索引在每个维度上增加1时，必须跳过的存储中的元素数量。
存储偏移量	storage offset	存储中对应于张量中第一个元素的index。

$$张量偏移、形状（大小）和步长$$

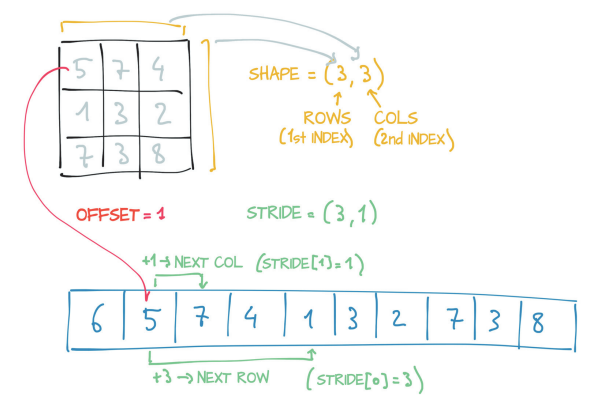
上图例子中，在二维张量中访问元素$(i, j)$的结果是访问存储中元素的索引如下计算：

$$index((i, j)) = storage\_offset + stride[0] * i + stride[1] * j$$

更加广义的：对于形状为$shape(d1, d2,.., dn)$的张量的视图中的元素$E(e1, e2,…,en)$，如果该张量的存储的步长为 $stride(s1, s2,…,sn)$ 、存储偏移量为 $s_o$，那么元素$E$的存储位置$index$是：

$$index(E(e1, e2,...,en)) = s\_o + s1 * e1 + s2 * e2 + ... + sn *en$$

由此我们看出张量视图中的元素由受以下因素影响：

$$张量视图 = f(张量存储, 张量形状, 张量步长, 张量偏移)$$

张量存储对张量操作的影响

这种张量和存储之间的间接性导致了一些操作，比如转置一个张量或者提取一个次张量，这些操作是便宜的（消耗很少资源），因为它们不会导致内存的重新分配；而是，它们包括分配一个新的张量对象，这个张量对象的形状、存储偏移量或步长有不同的值。

子张量的维数变少，而索引的存储空间仍然和原来的点张量一样。改变子张量会对原张量产生副作用（对子张量的修改会影响原张量）。但是这种效果可能并不总是存在，因为可以把子张量克隆成一个新的张量。

没有分配新的内存：只有通过创建一个新的张量实例来获得转置（transpose），这个张量实例的步长与原来的张量不同。可以通过张量的重新布局函数，比如PyTorch中的contiguous()函数，来强制拷贝一份张量，让它的布局和从新创建的张量一样。

$$张量的转置操作$$

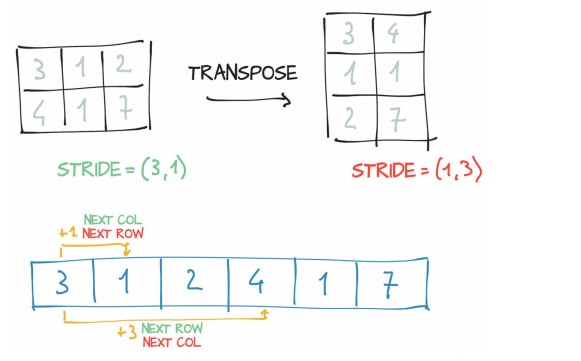
张量的视图与存储的区别与联系

联系

对于形状为$shape(d1, d2,.., dn)$的张量的视图中的元素$E(e1, e2,…,en)$，如果该张量的存储的步长为 $stride(s1, s2,…,sn)$ 、存储偏移量为 $s_o$，那么元素$E$的存储位置$index$是：

$$index(E(e1, e2,...,en)) = s\_o + s1 * e1 + s2 * e2 + ... + sn *en$$

张量视图中的元素由受以下因素影响：

$$张量视图 = f(张量存储, 张量形状, 张量步长, 张量偏移)$$

区别

• 相同存储可以有不同的视图：tensor_B.storage() 与 tensor_B_transpose.storage() 相同，但是 tensor_B 与 tensor_B_transpose 不同。
• 相同的视图可以有不同的存储：tensor_A 与 tensor_B_transpose 相同，但是 tensor_A.storage() 与 tensor_B_transpose.storage() 不同。

总结：张量的视图与存储通过索引来建立关系，它们之间没有必然性，即相同存储可以有不同的视图，相同的视图可以有不同的存储。

张量的数据类型和操作

结合该文件理解以下内容：TensorFlow张量的常用操作.ipynb ，下面是该文件的主要内容：

• 数据类型：dtype=int32, float32, string, bool
• 创建张量：tf.convert_to_tensor, tf.constant, tf.zeros, tf.ones, tf.zeros_like, tf.fill, tf.random.normal, tf.random.uniform, tf.range
• 索引与切片：A[1][2][1], A[1, 2, 1], A[ :, :, 0:3:2], A[..., 0:3:2]
• 维度变换：tf.reshape, tf.expand_dims, tf.squeeze, tf.transpose
• 数据复制：tf.tile
• 数学运算：+, -, *, /, //, %, **, tf.pow, tf.square, tf.sqrt, tf.math.log, tf.matmul, @
• 合并与分割：tf.concat, tf.stack, tf.split, tf.unstack
• 统计量：tf.norm, tf.reduce_max min mean sum, tf.argmax, tf.argmin
• 张量比较：tf.equal
• 填充与复制：tf.pad, tf.keras.preprocessing.sequence.pad_sequences, tf.tile
• 数据限幅：tf.maximum, tf.minimum, tf.clip_by_value
• 数据收集：tf.gather, tf.gather_nd
• 掩码：tf.boolean_mask
• 条件：tf.where
• 数据刷新：tf.scatter_nd
• 采样：tf.meshgrid

TODO：增加PyTorch版本张量的操作

数值类型

1. 标量，0维张量，主要用于模型损失和各种测量指标的表示，比如准确率、精度等；
2. 向量，1维张量，主要用于表示模型权重中的偏置b；
3. 矩阵，2维张量，主要用于表示线性模型Dense中的权重矩阵W；
4. 张量，3维张量主要用于序列数据，它的格式是 [batch_size, sequence length, feature length]，比如自然语言处理中句子的嵌入表示 [批量大小，句子长度，词嵌入维度]。4维张量主要用于图像数据，它的格式是 [batch_size, length, width, channel]。更高维度张量较少使用。

张量操作的意义

神经网络为什么要使用使用偏置b？

感性认识：

1. 神经网络中的偏置（bias）究竟有这么用？
2. 神经网络中的偏置项b到底是什么？

进一步认识：简单来说，“仿射变换”就是：“线性变换”+“平移”。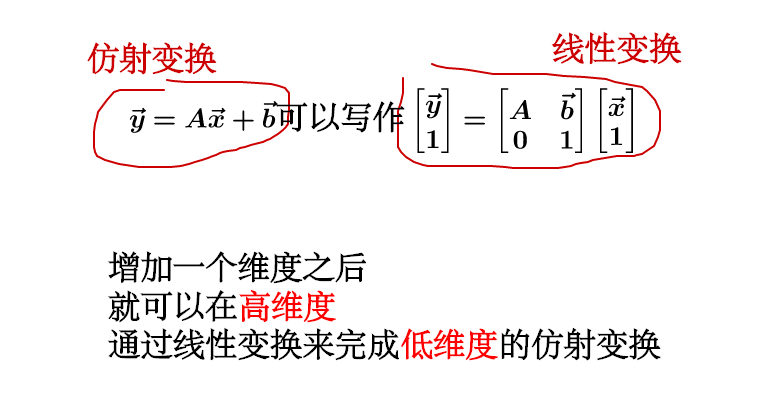

神经网络需要仿射变换（常常再仿射变换后加上一个非线性的激活函数），所以可以巧妙地在输入时增加一个维度（通常设置为1），把仿射变换转换成了线性变换，从而简化了计算。

阅读：

1. 仿射变换
2. 旋转变换（一）旋转矩阵

内积（点积、数量积）

内积-百度百科
点积在数学中，又称数量积（dot product; scalar product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
两个向量$a = [a_1, a_2,…, a_n]$和$b = [b_1, b_2,…, b_n]$的点积定义为：
$a \cdot b = a_1b_1 + a_2b_2 + … + a_nb_n$。
使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：
$a \cdot b = (a^T) * b$，这里的$a^T$指示矩阵a的转置。

外积（向量积）

外积-百度百科外积一般指两个向量的向量积；或在几何代数中，指有类似势的运算如楔积。这些运算的势是笛卡尔积的势。这个名字与内积相对，它是有相反次序的积。这里写的是外积，但是下面的写的是矢量积。

定义
把向量外积定义为：
符号表示：$a \times b$
大小：$|a|·|b|·sin$.
方向：右手定则：若坐标系是满足右手定则的，设 $z=x \times y, |z|=|x||y| * sin$；则x,y,z构成右手系，伸开右手手掌，四个手指从x轴正方向方向转到y轴正方面，则大拇指方向即为z正轴方向。
外积的坐标表示：
$(x_1,y_1,z_1) \times (x_2,y_2,z_2)=(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1)$

张量与现实数据的转换

结合该文件理解以下内容：用张量来表示现实世界的数据.ipynb，下面是该文件的主要内容：

• 将不同类型的实际数据表示为PyTorch张量
• 处理各种数据类型，包括电子表格、时间序列、文本、图像、医疗成像、视频、音频
• 从文件中加载数据
• 将数据转换为张量
• 对张量进行整形（shaping），使其可以用作神经网络模型的输入