阅读本篇前，最好先阅读多层感知机的反向传播算法。反向传播的基础知识和符号定义都在该文章中。
卷积神经网络：前向传播算法
CNN输入层前向传播到卷积层
输入层的前向传播是CNN前向传播算法的第一步。一般输入层对应的都是卷积层。
改进神经网络的学习方法——弃权
改进神经网络的学习方法——正则化
改进神经网络的学习方法——Softmax
改进神经网络的学习方法——交叉熵
交叉熵
交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。
交叉熵的定义
交叉熵的应用
- 交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。
- 在特征工程中，可以用来衡量两个随机变量之间的相似度。
- 在语言模型中（NLP）中，由于真实的分布p是未知的，在语言模型中，模型是通过训练集得到的，交叉熵就是衡量这个模型在测试集上的正确率。
贝叶斯估计、最大似然估计、最大后验估计三者的区别
实例分析
即使学过机器学习的人，对机器学习中的 MLE(极大似然估计)、MAP(最大后验估计)以及贝叶斯估计(Bayesian) 仍有可能一知半解。对于一个基础模型，通常都可以从这三个角度去建模，比如对于逻辑回归（Logistics Regression）来说：
使用神经网络识别手写数字——代码实现
部分代码解读
在之前描述 MNIST 数据时，我说它分成了 60,000 个训练图像和 10,000 个测试图像。这是官方的 MNIST 的描述。实际上，我们将用稍微不同的方法对数据进行划分。我们将测试集保持原样，但是将 60,000 个图像的 MNIST 训练集分成两个部分：一部分 50,000 个图像，我们将用来训练我们的神经网络，和一个单独的 10,000 个图像的验证集。在本章中我们不使用验证数据，但是在本书的后面我们将会发现它对于解决如何去设置某些神经网络中的超参数是很有用的，例如学习率等，这些参数不被我们的学习算法直接选择。尽管验证数据不是原始 MNIST 规范的一部分，然而许多人以这种方式使用 MNIST，并且在神经网络中使用验证数据是很普遍的。从现在起当我提到“MNIST 训练数据”时，我指的是我们的 50,000 个图像数据集，而不是原始的 60,000图像数据集
使用神经网络识别手写数字——梯度下降算法
原文链接：CHAPTER 1 Using neural nets to recognize handwritten digits
神经网络的架构
假设我们有这样的网络：
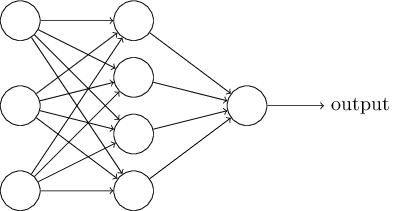
前面提过，这个网络中最左边的称为输入层，其中的神经元称为输入神经元。最右边的，即输出层包含有输出神经元，在本例中，输出层只有一个神经元。中间层，既然这层中的神经元既不是输入也不是输出，则被称为隐藏层。“隐藏”这一术语也许听上去有些神秘，我第一次听到这个词，以为它必然有一些深层的哲学或数学涵意，但它实际上仅仅意味着“既非输入也非输出”。上面的网络仅有一个隐藏层，但有些网络有多个隐藏层。例如，下面的四层网络
有两个隐藏层：
使用神经网络识别手写数字——感知器
原文链接：CHAPTER 1 Using neural nets to recognize handwritten digits
本书序言
在传统的编程方法中，我们告诉计算机做什么，把大问题分成许多小的、精确定义的任务，计算机可以很容易地执行。相比之下，在神经网络中，我们不告诉计算机如何解决我们的问题。相反，它从观测数据中学习，找出它自己的解决问题的方法。