为什么选择神经网络的超参数是个难题
直到现在,我们还没有解释对诸如学习率 $\eta$,正则化参数 $\lambda$ 等等超参数选择的方法。我只是给出那些效果很好的值而已。实践中,当你使用神经网络解决问题时,寻找好的超参数其实是很困难的一件事。例如,我们要解决 MNIST 问题,开始时对于选择什么样的超参数一无所知。假设,刚开始的实验中选择前面章节的参数都是运气较好。但在使用学习率 $\eta=10.0$ 而正则化参数 $\lambda=1000.0$。下面是我们的一个尝试:
1 | import mnist_loader |
我们分类准确率并不比随机选择更好。网络就像随机噪声产生器一样。
你可能会说,“这好办,降低学习率和正则化参数就好了。”不幸的是,你并不先验地知道这些就是需要调整的超参数。可能真正的问题出在 $30$ 个隐藏元中,本身就不能很有效,不管我们如何调整其他的超参数都没有作用的?可能我们真的需要至少 $100$ 个隐藏神经元?或者是 $300$ 个隐藏神经元?或者更多层的网络?或者不同输出编码方式?可能我们的网络一直在学习,只是学习的回合还不够?可能 minibatch 设的太小了?可能我们需要切换成二次代价函数?可能我们需要尝试不同的权重初始化方法?等等。很容易就在超参数的选择中迷失了方向。如果你的网络规模很大,或者使用了很多的训练数据,这种情况就很令人失望了,因为一次训练可能就要几个小时甚至几天乃至几周,最终什么都没有获得。如果这种情况一直发生,就会打击你的自信心。可能你会怀疑神经网络是不是适合你所遇到的问题?可能就应该放弃这种尝试了?
本节,我会给出一些用于设定超参数的启发式想法。目的是帮你发展出一套工作流来确保很好地设置超参数。当然,我不会覆盖超参数优化的每个方法。那是太繁重的问题,而且也不会是一个能够完全解决的问题,也不存在一种通用的关于正确策略的共同认知。总是会有一些新的技巧可以帮助你提高一点性能。但是本节的启发式想法能帮你开个好头。
宽泛策略(Broad strategy)
在使用神经网络来解决新的问题时,一个挑战就是获得任何一种非寻常的学习,也就是说,达到比随机的情况更好的结果。这个实际上会很困难,尤其是遇到一种新类型的问题时。让我们看看有哪些策略可以在面临这类困难时候尝试。
假设,我们第一次遇到 MNIST 分类问题。刚开始,你很有激情,但是当第一个神经网络完全失效时,你会觉得有些沮丧。此时就可以将问题简化。丢开训练和验证集合中的那些除了$0$ 和 $1$ 的那些图像。然后试着训练一个网络来区分 $0$ 和 $1$。不仅仅问题比 $10$个分类的情况简化了,同样也会减少 80% 的训练数据,这样就给出了 $5$ 倍的加速。这样可以保证更快的实验,也能给予你关于如何构建好的网络更快的洞察。
你通过简化网络来加速实验进行更有意义的学习。如果你相信 $[784, 10]$ 的网络更可能比随机更加好的分类效果,那么就从这个网络开始实验。这会比训练一个 $[784, 30 ,10]$的网络更快,你可以进一步尝试后一个。
你可以通过提高监控的频率来在试验中获得另一个加速了。
我们可以继续,逐个调整每个超参数,慢慢提升性能。一旦我们找到一种提升性能的 $\eta$ 值,我们就可以尝试寻找好的值。然后按照一个更加复杂的网络架构进行实验,假设是一个有 $10$ 个隐藏元的网络。然后继续调整 $\eta$ 和 $\lambda$。接着调整成 $20$ 个隐藏元。然后将其他的超参数调整再调整。如此进行,在每一步使用我们 hold out 验证数据集来评价性能,使用这些度量来找到越来越好的超参数。当我们这么做的时候,一般都需要花费更多时间来发现由于超参数改变带来的影响,这样就可以一步步减少监控的频率。
所有这些作为一种宽泛的策略看起来很有前途。然而,我想要回到寻找超参数的原点。实际上,即使是上面的讨论也传达出过于乐观的观点。实际上,很容易会遇到神经网络学习不到任何知识的情况。你可能要花费若干天在调整参数上,仍然没有进展。 所以我想要再重申一下在前期你应该从实验中尽可能早的获得快速反馈。 直觉上看,这看起来简化问题和架构仅仅会降低你的效率。实际上,这样能够将进度加快,因为你能够更快地找到传达出有意义的信号的网络。一旦你获得这些信号,你可以尝尝通过微调超参数获得快速的性能提升。这和人生中很多情况一样,万事开头难。
好了,上面就是宽泛的策略。现在我们看看一些具体的设置超参数的推荐。我会聚焦在学习率 $\eta$,L2 regularization参数 $\lambda$,和小批量数据大小。然而,很多的观点同样可以应用在其他的超参数的选择上,包括一些关于网络架构的、其他类型的regularization和一些本书后面遇到的如 momentum co-efficient 这样的超参数。
学习速率(Learning rate)
假设我们运行了三个不同学习速率($\eta=0.025$、$\eta=0.25$、$\eta=2.5$)的 MNIST 网络。我们会像前面介绍的实验那样设置其他的超参数,进行 $30$ 回合,minibatch 大小为 $10$,然后 $\lambda = 5.0$。我们同样会使用整个 $50,000$ 幅训练图像。下面是一副展示了训练代价的变化情况的图:
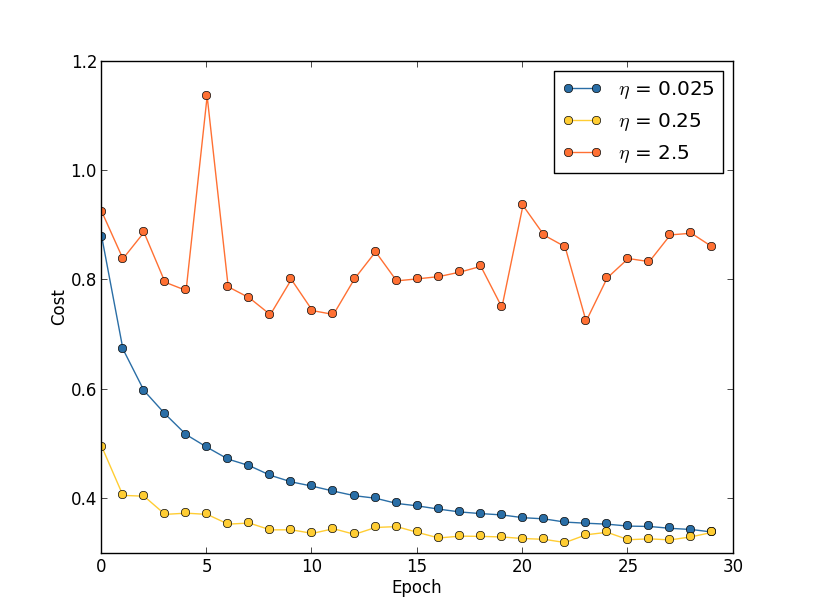
使用 $\eta=0.025$,代价函数平滑下降到最后的回合。使用 $\eta=0.25$,代价刚开始下降,在大约 $20$ 回合后接近饱和状态,后面就是微小的震荡和随机抖动。最终使用 $\eta=2.5$ 代价从始至终都震荡得非常明显。为了理解震荡的原因,回想一下随机梯度下降其实是期望我们能够逐渐地抵达代价函数的谷底的,
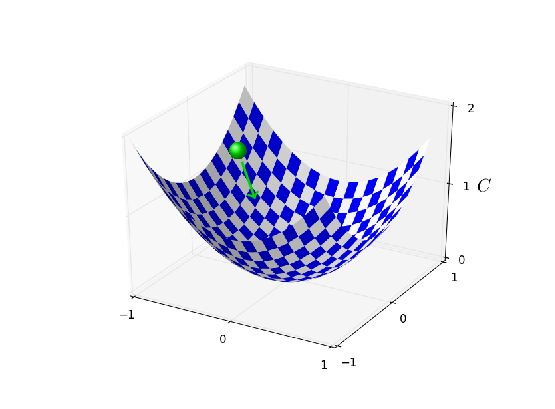
然而,如果 $\eta$ 太大的话,步长也会变大可能会使得算法在接近最小值时候又越过了谷底。这在 $\eta=2.5$ 时非常可能发生。当我们选择 $\eta=0.25$ 时,初始几步将我们带到了谷底附近,但一旦到达了谷底,又很容易跨越过去。而在我们选择 $\eta=0.025$ 时,在前 $30$ 回合的训练中不再受到这个情况的影响。当然,选择太小的%学习速率,也会带来另一个题,\gls*{sgd}算法变慢了。一种更加好的策略其实是,在开始时使用 $\eta=0.25$,随着越来越接近谷底,就换成$\eta=0.025$。这种可变学习速率的方法我们后面会介绍。现在,我们就聚焦在找出一个单独的好的学习速率的选择,$\eta$。
所以,有了这样的想法,我们可以如下设置 $\eta$。
首先,我们选择在训练数据上的代价立即开始下降而非震荡或者增加时作为 $\eta$ 的阈值的估计。这个估计并不需要太过精确。你可以估计这个值的量级,比如说从 $\eta=0.01$ 开始。如果代价在训练的前面若干回合开始下降,你就可以逐步地尝试 $\eta=0.1, 1.0,…$,直到你找到一个 $\eta$ 的值使得在开始若干回合代价就开始震荡或者增加。
相反,如果代价在 $\eta=0.01$ 时就开始震荡或者增加,那就尝试 $\eta=0.001, 0.0001,…$ 直到你找到代价在开始回合就下降的设定。按照这样的方法,我们可以掌握学习速率的阈值的量级的估计。你可以选择性地优化估计,选择那些最大的 $\eta$,比方说 $\eta=0.5$ 或者 $\eta=0.2$(这里也不需要过于精确)。
显然,$\eta$ 实际值不应该比阈值大。实际上,如果 $\eta$ 的值重复使用很多回合的话,你更应该使用稍微小一点的值,例如,阈值的一半这样的选择。这样的选择能够允许你训练更多的回合,不会减慢学习的速度。
在 MNIST 数据中,使用这样的策略会给出一个关于学习速率 $\eta$ 的一个量级的估计,大概是 $0.1$。在一些改良后,我们得到了阈值 $\eta=0.5$。所以,我们按照刚刚的取一半的策略就确定了学习速率为 $\eta=0.25$。实际上,我发现使用 $\eta=0.5$ 在 $30$ 回合内表现是很好的,所以选择更低的学习速率,也没有什么问题。
为什么使用代价函数来选择学习速率?而不是验证集
这看起来相当直接。然而,使用训练代价函数来选择 $\eta$ 看起来和我们之前提到的通过验证集来确定超参数的观点有点矛盾。实际上,我们会使用验证准确率来选择正则化超参数,minibatch 大小,和层数及隐藏元个数这些网络参数,等等。为何对学习速率要用不同的方法呢?坦白地说,这些选择其实是我个人美学偏好,个人习惯罢了。原因就是其他的超参数倾向于提升最终的测试集上的分类准确率,所以将他们通过验证准确率来选择更合理一些。然而,学习速率仅仅是偶然地影响最终的分类准确率的。学习率主要的目的是控制梯度下降的步长,监控训练代价是最好的检测步长过大的方法。 所以,这其实就是个人的偏好。在学习的前期,如果验证准确率提升,训练代价通常都在下降。所以在实践中使用那种衡量方式并不会对判断的影响太大。
学习速率调整
我们一直都将学习速率设置为常量。但是,通常采用可变的学习速率更加有效。在学习的前期,权重可能非常糟糕。所以最好是使用一个较大的学习速率让权重变化得更快。越往后,我们可以降低学习速率,这样可以作出更加精良的调整。
我们要如何设置学习速率呢?其实有很多方法。一种自然的观点是使用提前终止的想法。就是保持学习速率为一个常量直到验证准确率开始变差。然后按照某个量下降学习速率,比如说按照$10$ 或者 $2$。我们重复此过程若干次,直到学习速率是初始值的 $1/1024$(或者$1/1000$)。那时就终止。
可变学习速率可以提升性能,但是也会产生大量可能的选择。这些选择会让人头疼~——~你可能需要花费很多精力才能优化学习规则。对刚开始实验,我建议使用单一的常量作为学习速率的选择。这会给你一个比较好的近似。后面,如果你想获得更好的性能,值得按照某种规则进行实验,根据我已经给出的资料。
提前停止 来确定训练的周期的数量
正如我们在本章前面讨论的那样,提前停止表示在每个回合的最后,我们都要计算验证集上的分类准确率。当准确率不再提升,就终止它。这让选择回合数变得很简单。特别地,也意味着我们不再需要担心显式地掌握回合数和其他超参数的关联。而且,这个过程还是自动的。另外,提前停止也能够帮助我们避免过拟合。尽管在实验前期不采用提前停止,这样可以看到任何过匹配的信号,使用这些来选择正则化方法,但提前停止仍然是一件很棒的事。
我们需要再明确一下什么叫做分类准确率不再提升,这样方可实现提前停止。正如我们已经看到的,分类准确率在整体趋势下降的时候仍旧会抖动或者震荡。如果我们在准确度刚开始下降的时候就停止,那么肯定会错过更好的选择。一种不错的解决方案是如果分类准确率在一段时间内不再提升的时候终止。例如,我们要解决 MNIST 问题。如果分类准确度在近$10$ 个回合都没有提升的时候,我们将其终止。这样不仅可以确保我们不会终止得过快,也能够使我们不要一直干等直到出现提升。
这种 $10$ 回合不提升就终止的规则很适合 MNIST 问题的一开始的探索。然而,网络有时候会在很长时间内于一个特定的分类准确率附近形成平缓的局面,然后才会有提升。如果你尝试获得相当好的性能,这个规则可能就会太过激进了~——~停止得太草率。所以,我建议在你更加深入地理解网络训练的方式时,仅仅在初始阶段使用 $10$ 回合不提升规则,然后逐步地选择更久的回合,比如说:$20$ 回合不提升就终止,$50$ 回合不提升就终止,以此类推。当然,这就引入了一种新的需要优化的超参数!实践中,其实比较容易设置这个超参数来获得相当好的结果。类似地,对不同于 MNIST 的问题,$10$ 回合不提升就终止的规则会太过激进或者太过保守,这都取决于问题本身的特质。然而,进行一些小的实验,发现好的提前终止的策略还是非常简单的。
我们还没有在我们的 MNIST 实验中使用提前终止。原因是我们已经比较了不同的学习观点。这样的比较其实比较适合使用同样的训练回合。但是,在 network2.py 中实现提前终止还是很有价值的:
小批量数据的大小
我们应该如何设置小批量数据的大小?为了回答这个问题,让我们先假设正在进行在线学习,也就是说使用大小为 $1$ 的小批量数据。
一个关于在线学习的担忧是使用只有一个样本的小批量数据会带来关于梯度的错误估计。实际上,误差并不会真的产生这个问题。原因在于单一的梯度估计不需要绝对精确。我们需要的是确保代价函数保持下降的足够精确的估计。就像你现在要去北极点,但是只有一个不大精确的(差个 $10-20$ 度)指南针。如果你不断频繁地检查指南针,指南针会在平均状况下给出正确的方向,所以最后你也能抵达北极点。
基于这个观点,这看起来好像我们需要使用在线学习。实际上,情况会变得更加复杂。在上一章的问题中我指出我们可以使用矩阵技术来对所有在小批量数据中的样本同时计算梯度更新,而不是进行循环。所以,取决于硬件和线性代数库的实现细节,这会比循环方式进行梯度更新快好多。也许是 $50$ 和 $100$ 倍的差别。
现在,看起来这对我们帮助不大。我们使用 $100$ 的小批量数据的学习规则如下;
这里是对小批量数据中所有训练样本求和。而在线学习是
即使它仅仅是 $50$ 倍的时间,结果仍然比直接在线学习更好,因为我们在线学习更新得太过频繁了。假设,在小批量数据下,我们将学习率扩大了 $100$ 倍,更新规则就是
这看起来像做了 $100$ 次独立的在线学习。但是仅仅花费了 $50$ 次在线学习的时间。当然,其实不是同样的 100 次在线学习,因为小批量数据中 $\nabla C_x$ 是都对同样的权重进行衡量的,而在线学习中是累加的学习。使用更大的小批量数据看起来还是显著地能够进行训练加速的。
所以,选择最好的小批量数据大小也是一种折衷。太小了,你不会用上很好的矩阵库的快速计算。太大,你是不能够足够频繁地更新权重的。你所需要的是选择一个折衷的值,可以最大化学习的速度。 幸运的是,小批量数据大小的选择其实是相对独立的一个超参数(网络整体架构外的参数),所以你不需要优化那些参数来寻找好的小批量数据大小。因此,可以选择的方式就是使用某些可以接受的值(不需要是最优的)作为其他参数的选择,然后进行不同小批量数据大小的尝试,像上面那样调整 $\eta$。画出验证准确率的值随时间(非回合)变化的图,选择哪个得到最快性能的提升的小批量数据大小。得到了小批量数据大小,也就可以对其他的超参数进行优化了。
当然,你也发现了,我这里并没有做到这么多。实际上,我们的实现并没有使用到小批量数据更新快速方法。就是简单使用了小批量数据大小为 $10$。所以,我们其实可以通过降低小批量数据大小来进行提速。我也没有这样做,因为我希望展示小批量数据大于$1$ 的使用,也因为我实践经验表示提升效果其实不明显。在实践中,我们大多数情况肯定是要实现更快的小批量数据更新策略,然后花费时间精力来优化小批量数据大小,来达到总体的速度提升。
自动技术:
我已经给出很多在手动进行超参数优化时的启发式规则。手动选择当然是种理解网络行为的方法。不过,现实是,很多工作已经使用自动化过程进行。通常的技术就是网格搜索,可以系统化地对超参数的参数空间的网格进行搜索。网格搜索的成就和限制(易于实现的变体)在 James Bergstra 和 Yoshua Bengio $2012$年的论文作者为 James Bergstra 和 Yoshua Bengio(2012)。中已经给出了综述。很多更加精细的方法也被大家提出来了。
总结
跟随上面的经验并不能帮助你的网络给出绝对最优的结果。但是很可能给你一个好的开始和一个改进的基础。特别地,我已经非常独立地讨论了超参数的选择。实践中,超参数之间存在着很多关系。你可能使用 $\eta$ 进行试验,发现效果不错,然后去优化 $\lambda$,发现这里又和 $\eta$ 混在一起了。在实践中,一般是来回往复进行的,最终逐步地选择到好的值。总之,启发式规则其实都是经验,不是金规玉律。你应该注意那些没有效果的尝试的信号,然后乐于尝试更多试验。特别地,这意味着需要更加细致地监控神经网络的行为,特别是验证集上的准确率。
选择超参数的难度在于如何选择超参数的方法太分散, 这些方法分散在许多的研究论文,软件程序甚至仅仅在一些研究人员的大脑中, 因而变得更加困难。很多很多的论文给出了(有时候矛盾的)建议。
设定超参数的挑战让一些人抱怨神经网络相比较其他的机器学习算法需要大量的工作进行参数选择。我也听到很多不同的版本:“的确,参数完美的神经网络可能会在这问题上获得最优的性能。但是,我可以尝试一下随机森林(或者 SVM 或者……这里脑补自己偏爱的技术)也能够工作的。我没有时间搞清楚那个最好的神经网络。” 当然,从一个实践者角度,肯定是应用更加容易的技术。这在你刚开始处理某个问题时尤其如此,因为那时候,你都不确定一个机器学习算法能够解决那个问题。但是,如果获得最优的性能是最重要的目标的话,你就可能需要尝试更加复杂精妙的知识的方法了。如果机器学习总是简单的话那是太好不过了,但也没有什么理由说机器学习非得这么简单。
参考文献
[1] Michael Nielsen. CHAPTER 3 Improving the way neural networks learn[DB/OL]. http://neuralnetworksanddeeplearning.com/chap3.html, 2018-06-28.
[2] Zhu Xiaohu. Zhang Freeman. Another Chinese Translation of Neural Networks and Deep Learning[DB/OL]. https://github.com/zhanggyb/nndl/blob/master/chap3.tex, 2018-06-28.

