二分类、多分类、多标签和多输出问题解析

本文分为理论和实验两部分：

• 理论部分先讲解二分类、多分类与多标签分类问题的基本概念，然后分析它们为什么使用不同的激活函数和损失函数，结论见文末总结。

• 实验部分重点讲解了多标签和多输出问题。

二分类、多分类、多标签和多输出问题的基本概念

二分类：表示分类任务中有两个类别，比如我们想识别一幅图片是不是猫。也就是说，训练一个分类器，输入一幅图片，用特征向量x表示，输出是不是猫，用y=0或1表示。二类分类是假设每个样本都被设置了一个且仅有一个标签 0 或者 1。

多类分类(Multiclass classification): 表示分类任务中有多个类别, 比如对一堆水果图片分类, 它们可能是橘子、苹果、梨等. 多类分类是假设每个样本都被设置了一个且仅有一个标签: 一个水果可以是苹果或者梨, 但是同时不可能是两者。

多标签分类(Multilabel classification): 给每个样本一系列的目标标签. 可以想象成一个数据点的各属性不是相互排斥的(一个水果既是苹果又是梨就是相互排斥的), 比如一个文档相关的话题. 一个文本可能被同时认为是宗教、政治、金融或者教育相关话题。

多输出分类：多个多分类或多标签分类组合输出的分类。网络至少会分支两次（有时候会更多），从而在网络末端创建出多组全连接头——然后你的网络的每个头都会预测一组类别标签，使其有可能学习到不相交的标签组合。比如一个网络同时预测服饰的款式类型和颜色类型。

多分类问题与二分类问题关系

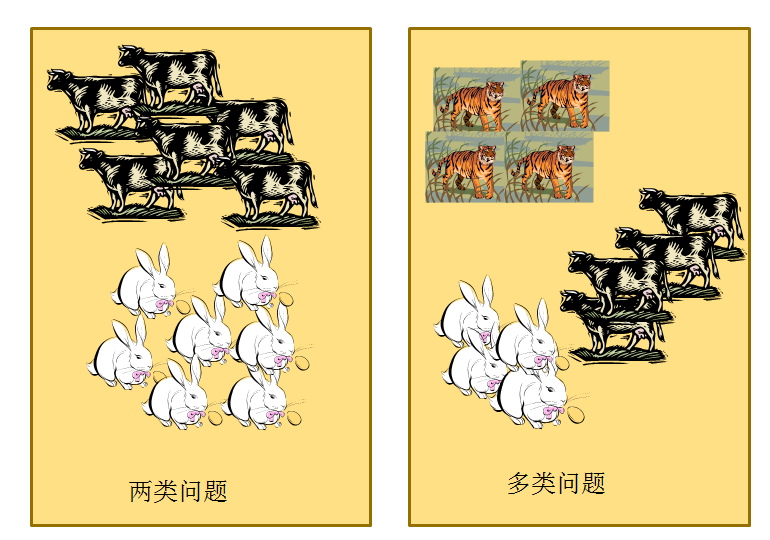
首先，两类问题是分类问题中最简单的一种。其次，很多多类问题可以被分解为多个两类问题进行求解（请看下文分解）。所以，历史上有很多算法都是针对两类问题提出的。下面我们来分析如何处理多分类问题：

直接分成多类

比如使用 Softmax 回归。

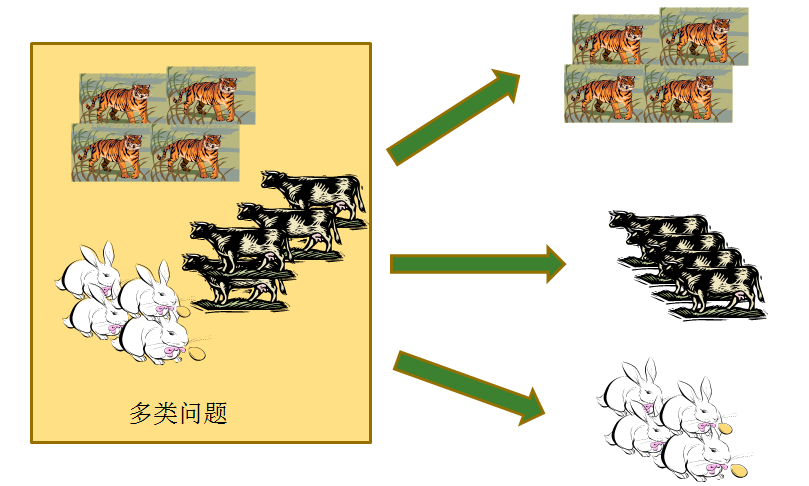
一对一的策略

给定数据集D这里有N个类别，这种情况下就是将这些类别两两配对，从而产生N(N−1)2个二分类任务，在测试的时候把样本交给这些分类器，然后进行投票。

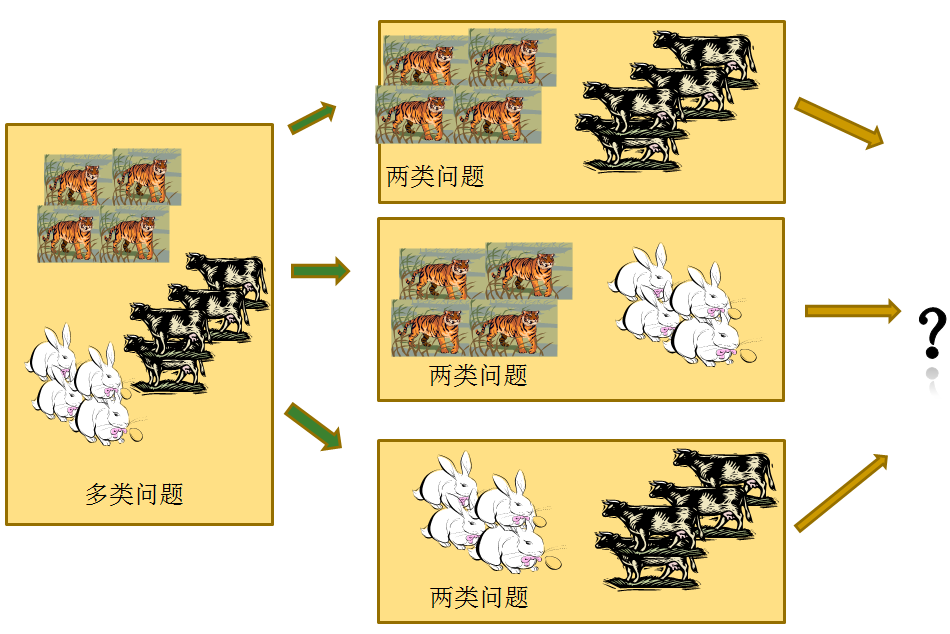
一对其余策略

将每一次的一个类作为正例，其余作为反例，总共训练N个分类器。测试的时候若仅有一个分类器预测为正的类别则对应的类别标记作为最终分类结果，若有多个分类器预测为正类，则选择置信度最大的类别作为最终分类结果。

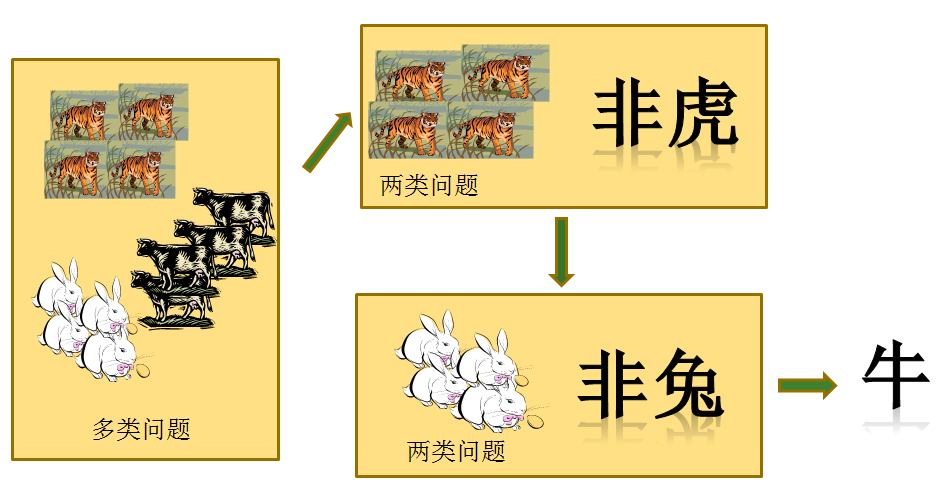
多标签问题与二分类问题关系

面临的问题：
图片的标签数目不是固定的，有的有一个标签，有的有两个标签，但标签的种类总数是固定的，比如为5类。

解决该问题：
采用了标签补齐的方法，即缺失的标签全部使用0标记，这意味着，不再使用one-hot编码。例如：标签为：-1,1,1,-1,1 ;-1表示该类标签没有，1表示该类标签存在，则这张图片的标签编码为：

0 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 1

2.如何衡量损失？

计算出一张图片各个标签的损失，然后取平均值。

3.如何计算精度

计算出一张图片各个标签的精度，然后取平均值。

该处理方法的本质：把一个多标签问题，转化为了在每个标签上的二分类问题。

损失函数的选择问题

基于逻辑回归的二分类问题

对于logistic回归，有：

$$h_{\theta}(x) = g(\theta^{T}x) = \frac{1}{1+e^{-\theta^{T}x}}$$

逻辑回归有以下优点：

1. 它的输入范围是 $-\infty \to+\infty$，而之于刚好为（0，1），正好满足概率分布为（0，1）的要求。我们用概率去描述分类器，自然比单纯的某个阈值要方便很多；
2. 它是一个单调上升的函数，具有良好的连续性，不存在不连续点。

对数损失函数（logarithmic loss function) 或对数似然损失函数(log-likehood loss function) 。

$$L(Y,P(Y|X)) = -logP(Y|X)$$

逻辑回归中，采用的则是对数损失函数。根据上面的内容，我们可以得到逻辑回归的对数似然损失函数cost function：

$$cost(h_{\theta}(x),y) = \begin{cases} -log(h_{\theta}(x)) & \text {if y=1} \\ -log(1-h_{\theta}(x)) & \text{if y=0} \end{cases}$$

将以上两个表达式合并为一个，则单个样本的损失函数可以描述为：

$$cost(h_{\theta}(x),y) = -y_ilog(h_{\theta}(x)) - (1-y_i)log(1-h_{\theta}(x))$$

这就是逻辑回归最终的损失函数表达式。

基于 Softmax 的多分类问题

softmax层中的softmax 函数是logistic函数在多分类问题上的推广，它将一个N维的实数向量压缩成一个满足特定条件的N维实数向。压缩后的向量满足两个条件：

1. 向量中的每个元素的大小都在[0,1]
2. 向量所有元素的和为 1

因此，softmax适用于多分类问题中对每一个类别的概率判断，softmax的函数公式如下：

$$a^L_j = \frac {e^{z^L_j}}{\sum_k e^{z^L_k}}$$

基于 Softmax 的多分类问题采用的是 log似然代价函数（log-likelihood cost function）来解决。

单个样本的 log似然代价函数的公式为：

$$C = - \sum_i y_i log a_i$$

其中， $y_i$ 表示标签向量的第 $i$ 个分量。因为往往只有一个分量为 1 其余的分量都为 0，所以可以去掉损失函数中的求和符号，化简为，

$$C \equiv -\ln a_j$$

其中， $a_j$ 是向量 $y$ 中取值为 1 对应的第 $j$ 个分量的值。

交叉熵损失函数与 log 似然代价函数关系 本质一样

有的文献中也称 log 似然代价函数为交叉熵损失函数，这两个都是交叉熵损失函数，但是看起来长的却有天壤之别。为什么同是交叉熵损失函数，长的却不一样呢？

$$cost(h_{\theta}(x),y) = -y_ilog(h_{\theta}(x)) - (1-y_i)log(1-h_{\theta}(x))$$ $$C = - \sum_i y_i log a_i$$

因为这两个交叉熵损失函数对应不同的最后一层的输出。第一个对应的最后一层是 sigmoid，用于二分类问题，第二个对应的最后一层是 softmax，用于多分类问题。但是它们的本质是一样的，请看下面的分析。

首先来看信息论中交叉熵的定义：

$$-\int p(x)\text{log}g(x)dx$$

交叉熵是用来描述两个分布的距离的，神经网络训练的目的就是使 g(x) 逼近 p(x)。

sigmoid + 对数损失函数

先看看 sigmoid 作为神经网络最后一层的情况。sigmoid 作为最后一层输出的话，那就不能吧最后一层的输出看作成一个分布了，因为加起来不为 1。现在应该将最后一层的每个神经元看作一个分布，对应的 target 属于二项分布(target的值代表是这个类的概率)，那么第 i 个神经元交叉熵为

$$y_i\text{log}(h_{\theta})+(1-y_i)\text{log}(1-h_{\theta})$$

其实这个式子可以用求和符号改写，

$$C = - \sum_i log a_i$$

其中，

$$cost(h_{\theta}(x),y) = \begin{cases} -log(a_i) & a_i=h_{\theta} & \text {if } y_i=1 \\ -log(a_i) & a_i=1-h_{\theta} & \text{if } y_i=0 \end{cases}$$

Softmax + 交叉熵

现在来看 softmax 作为神经网络最后一层的情况。g(x)是什么呢？就是最后一层的输出 y 。p(x)是什么呢？就是我们的one-hot标签。我们带入交叉熵的定义中算一下，就会得到：

$$C = - \sum_i y_i log a_i$$

交叉熵损失函数与 log 似然损失函数的总结

注意到不管是交叉熵损失函数与 log 似然损失函数，交叉熵损失函数用于二分类问题， log 似然损失函数用于多分类，但是对于某一个样本只属于一个类别，只有一个标签。如果用 one-hot 编码样本的标签那么，对于标签向量只有一个分量的值为 1 其余的值都为 0。

所以不管是交叉熵损失函数与 log 似然损失函数，都可以化简为，

$$C \equiv -\ln a_j$$

其中， $a_j$ 是向量 $y$ 中取值为 1 对应的第 $j$ 个分量的值。这两个长的不一样的损失函数实际上是对应的不同的输出层。本质上是一样的。

我的建议是，采用 Kears 中的命名方法，对于二分类的交叉熵损失函数称之为 “二分类交叉熵损失函数（binary_crossentropy）” ，对于多分类的交叉熵损失函数称之为 “多类别交叉熵损失函数（categorical_crossentropy）”。

在 Kears 中也有提示（注意: 当使用categorical_crossentropy损失时，你的目标值应该是分类格式 (即，如果你有10个类，每个样本的目标值应该是一个10维的向量，这个向量除了表示类别的那个索引为1，其他均为0)。 为了将 整数目标值 转换为 分类目标值，你可以使用Keras实用函数to_categorical：）

---

一种更直接的证明方法，数学公式，

内容来源于 Hands-on Machine Learning with Scikit-Learn and TensorFlow 141 页。

多标签分类 + 二分类交叉熵损失函数

多标签问题与二分类问题关系在上文已经讨论过了，方法是计算一个样本各个标签的损失（输出层采用sigmoid函数），然后取平均值。把一个多标签问题，转化为了在每个标签上的二分类问题。

总结

分类问题名称	输出层使用激活函数	对应的损失函数
二分类	sigmoid函数	二分类交叉熵损失函数（binary_crossentropy）
多分类	Softmax函数	多类别交叉熵损失函数（categorical_crossentropy）
多标签分类	sigmoid函数	二分类交叉熵损失函数（binary_crossentropy）

为什么要引入多输出分类问题

使用Keras执行多标签分类非常简单，包括两个主要步骤：

使用 sigmoid 激活替换网络末端的 softmax 激活
换出明确的交叉熵的二进制交叉熵对你的损失函数
从那里你可以像往常一样训练你的网络。
应用上述过程的最终结果是多类分类器。
可以使用Keras多类分类来预测多个标签只是一个单一的向前传递。

但是，您需要考虑以下问题：

您需要针对要预测的每个类别组合的培训数据。

就像神经网络无法预测从未接受过训练的类一样，您的神经网络无法预测从未见过的组合的多个类别标签。这种行为的原因是由于网络内神经元的激活。

如果您的网络接受过（1）黑色裤子和（2）红色衬衫的示例训练，现在您想要预测“红裤子”（数据集中没有“红裤子”图像），负责检测的神经元“红色”和“裤子”会触发，但由于网络一旦到达完全连接的层之前从未见过这种数据/激活组合，您的输出预测很可能是不正确的（即，您可能会遇到“红色”或“裤子”，但两者都不太可能）。

同样，您的网络无法正确预测从未接受过培训的数据（您也不应该期望它）。在培训您自己的Keras网络进行多标签分类时，请牢记这一点。

使用多输出分类就可以解决此问题。通过创建两个全连接头和相关的子网络（如有必要），我们可以训练一个头分类服装种类，另一个头负责识别颜色——最终得到的网络可以分类「黑色裙子」，即使它之前从未在这样的数据上训练过！

---

多输出分类:针对服装类型和颜色的实验

实验详细指导

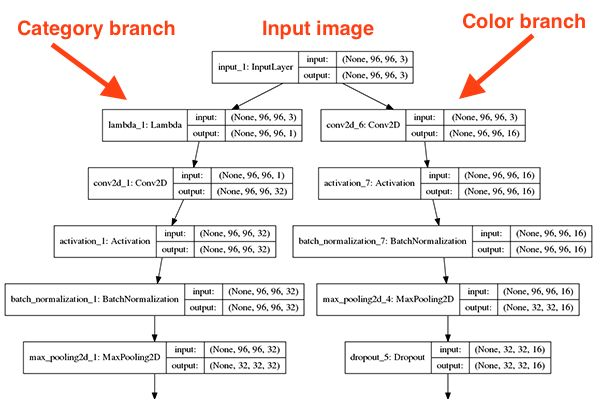
创建模型的关键代码

class FashionNet:
	@staticmethod
	def build_category_branch(inputs, numCategories,
		finalAct="softmax", chanDim=-1):
		# utilize a lambda layer to convert the 3 channel input to a
		# grayscale representation
		x = Lambda(lambda c: tf.image.rgb_to_grayscale(c))(inputs)

		# CONV => RELU => POOL
		x = Conv2D(32, (3, 3), padding="same")(x)
		x = Activation("relu")(x)
		x = BatchNormalization(axis=chanDim)(x)
		x = MaxPooling2D(pool_size=(3, 3))(x)
		x = Dropout(0.25)(x)

    # Omit some similar code

		# define a branch of output layers for the number of different
		# clothing categories (i.e., shirts, jeans, dresses, etc.)
		x = Flatten()(x)
		x = Dense(256)(x)
		x = Activation("relu")(x)
		x = BatchNormalization()(x)
		x = Dropout(0.5)(x)
		x = Dense(numCategories)(x)
		x = Activation(finalAct, name="category_output")(x)

		# return the category prediction sub-network
		return x

	@staticmethod
	def build_color_branch(inputs, numColors, finalAct="softmax",
		chanDim=-1):
		# CONV => RELU => POOL
		x = Conv2D(16, (3, 3), padding="same")(inputs)
		x = Activation("relu")(x)
		x = BatchNormalization(axis=chanDim)(x)
		x = MaxPooling2D(pool_size=(3, 3))(x)
		x = Dropout(0.25)(x)

    # Omit some similar code

		# define a branch of output layers for the number of different
		# colors (i.e., red, black, blue, etc.)
		x = Flatten()(x)
		x = Dense(128)(x)
		x = Activation("relu")(x)
		x = BatchNormalization()(x)
		x = Dropout(0.5)(x)
		x = Dense(numColors)(x)
		x = Activation(finalAct, name="color_output")(x)

		# return the color prediction sub-network
		return x

	@staticmethod
	def build(width, height, numCategories, numColors,
		finalAct="softmax"):
		# initialize the input shape and channel dimension (this code
		# assumes you are using TensorFlow which utilizes channels
		# last ordering)
		inputShape = (height, width, 3)
		chanDim = -1

		# construct both the "category" and "color" sub-networks
		inputs = Input(shape=inputShape)
		categoryBranch = FashionNet.build_category_branch(inputs,
			numCategories, finalAct=finalAct, chanDim=chanDim)
		colorBranch = FashionNet.build_color_branch(inputs,
			numColors, finalAct=finalAct, chanDim=chanDim)

		# create the model using our input (the batch of images) and
		# two separate outputs -- one for the clothing category
		# branch and another for the color branch, respectively
		model = Model(
			inputs=inputs,
			outputs=[categoryBranch, colorBranch],
			name="fashionnet")

		# return the constructed network architecture
		return model

实验输出

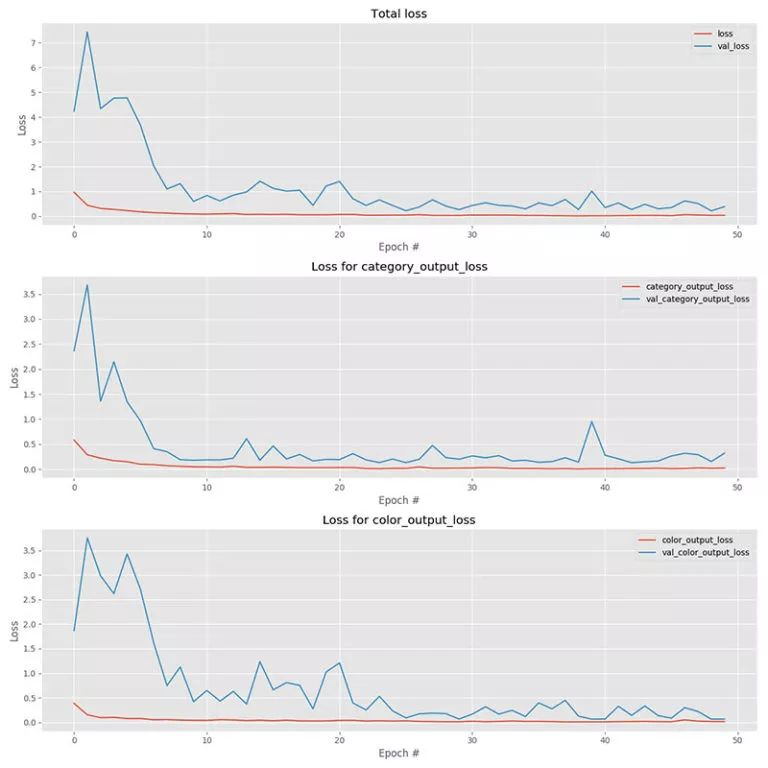
模型预测效果

---

参考文献

[1] François Chollet‏. Keras Document[DB/OL]. https://keras.io/, 2018-07-01.

[2] 目力过人. 多标签分类（multilabel classification ）[DB/OL]. https://blog.csdn.net/bemachine/article/details/10471383, 2018-07-01.

[3] Inside_Zhang.【联系】二项分布的对数似然函数与交叉熵（cross entropy）损失函数[DB/OL]. https://blog.csdn.net/lanchunhui/article/details/75433608, 2018-07-01.

[4] ke1th. 两种交叉熵损失函数的异同[DB/OL]. https://blog.csdn.net/u012436149/article/details/69660214, 2018-07-01.

[5] bitcarmanlee. logistic回归详解一：为什么要使用logistic函数[DB/OL]. https://blog.csdn.net/bitcarmanlee/article/details/51154481, 2018-07-01.

[6] Aurélien Géron. Hands-On Machine Learning with Scikit-Learn and TensorFlow[M]. America: O’Reilly Media, 2017-03-10, 140-141.

[7] Adrian Rosebrock. 使用Keras实现多输出分类：用单个模型同时执行两个独立分类任务[DB/OL]. https://www.jiqizhixin.com/articles/2018-08-14-2, 2018-08-18.