胶囊网络（Capsule Network）

胶囊网络的革命在于：它提出了一种新的“vector in vector out”的传递方案，并且这种方案在很大程度上是可解释的。

Hinton大神的胶囊网络

理解胶囊网络基本计算公式

将 Capsule 称作向量神经元 (vector neuron, VN)，而普通的人工神经元叫做标量神经元 (scalar neuron, SN)，下表总结了 VN 和 SN 之间的差异：

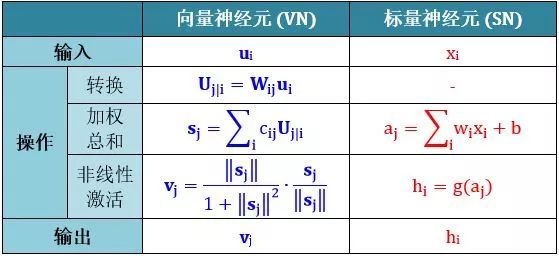
SN 从其他神经元接收输入标量，然后乘以标量权重再求和，然后将这个总和传递给某个非线性激活函数 (比如 sigmoid, tanh, Relu)，生出一个输出标量。该标量将作为下一层的输入变量。实质上，SN 可以用以下三个步骤来描述：

1. 将输入标量 x 乘上权重 w
2. 对加权的输入标量求和成标量 a
3. 用非线性函数将标量 a 转化成标量 h

VN 的步骤在 SN 的三个步骤前加一步：

1. 将输入向量 u 用矩阵 W 加工成新的输入向量 U
2. 将输入向量 U 乘上权重 c
3. 对加权的输入向量求和成向量 s
4. 用非线性函数将向量 s 转化成向量 v

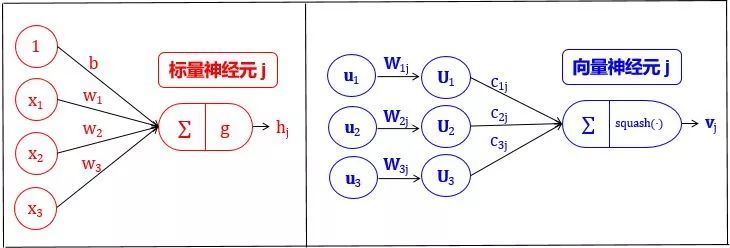
VN 和 SN 的过程总结如下图所示：

理解胶囊网络工作原理

这一小节分析计算公式的工作原理，为了使问题具体化，假设：

1. 上一层的 VN 代表眼睛 (u1), 鼻子 (u2) 和嘴巴 (u3)，称为低层特征。
2. 下一层第 j 个的 VN 代表脸，称为高层特征。注意下一层可能还有很多别的高层特征，脸是最直观的一个。

第一步：矩阵转化

• Uj|1 是根据眼睛位置来检测脸的位置
• Uj|2 是根据鼻子位置来检测脸的位置
• Uj|3 是根据嘴巴位置来检测脸的位置

现在，直觉应该是这样的：如果这三个低层特征 (眼睛，鼻子和嘴) 的预测指向相同的脸的位置和状态，那么出现在那个地方的必定是一张脸。如下图所示：

第二步：输入加权

这个步骤和标量神经元 SN 的加权形式有点类似。在 SN 的情况下，这些权重是通过反向传播 (backward propagation) 确定的，但是在 VN 的情况下，这些权重是使用动态路由 (dynamic routing) 确定的，具体算法见下面的动态路由小节 。本节只从高层面来解释动态路由，如下图：

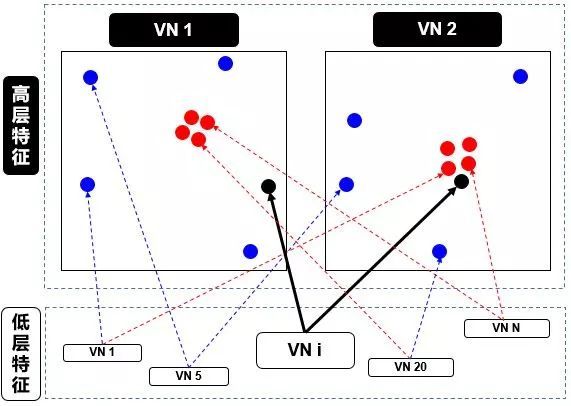
在上图中，我们有一个较低级别 VNi需要“决定”它将发送输出给哪个更高级别 VN1和 VN2。它通过调整权重 ci1和 ci2来做出决定。

现在，高级别 VN1和 VN2已经接收到来自其他低级别 VN 的许多输入向量，所有这些输入都以红点和蓝点表示。

• 红点聚集在一起，意味着低级别 VN 的预测彼此接近
• 蓝点聚集在一起，意味着低级别 VN 的预测相差很远

那么，低别级 VNi应该输出到高级别 VN1还是 VN2？这个问题的答案就是动态路由的本质。由上图看出

• VNi 的输出远离高级别 VN1 中的“正确”预测的红色簇
• VNi 的输出靠近高级别 VN2 中的“正确”预测的红色簇

而动态路由会根据以上结果产生一种机制，来自动调整其权重，即调高 VN2相对的权重 ci2，而调低 VN1相对的权重 ci1。

第三步：加权求和

这一步类似于普通的神经元的加权求和步骤，除了总和是向量而不是标量。加权求和的真正含义就是计算出第二步里面讲的红色簇心 (cluster centroid)。

第四步：非线性激活

这个公式的确是 VN 的一个创新，采用向量的新型非线性激活函数，又叫 squash 函数，姑且翻译成“压缩”函数。这个函数主要功能是使得 vj 的长度不超过 1，而且保持 vj和 sj同方向。

• 公式第一项压扁函数
• 如果 sj 很长，第一项约等于 1
• 如果 sj 很短，第一项约等于 0
• 公式第二项单位化向量 sj，因此第二项长度为 1

这样一来，输出向量 vj的长度是在 0 和 1 之间的一个数，因此该长度可以解释为 VN 具有给定特征的概率。

动态路由

低级别 VNi 需要决定如何将其输出向量发送到高级别 VNj，它是通过改变权重 cij而实现的。首先来看看 cij的性质：

1. 每个权重是一个非负值
2. 对于每个低级别 VNi，所有权重 cij 的总和等于 1
3. 对于每个低级别 VNi，权重的个数等于高级别 VN 的数量
4. 权重由迭代动态路由 (iterative dynamic routing) 算法确定

前两个性质说明 c 符合概率概念。VN 的长度被解释为它的存在概率。VN 的方向是其特征的参数化状态。因此，对于每个低级别 VNi，其权重 cij定义了属于每个高级别 VNj 的输出的概率分布。

一言以蔽之，低级别 VN 会将其输出发送到“同意”该输出的某个高级别 VN。这是动态路由算法的本质。很绕口是吧？分析完 Hinton 论文中的动态路由算法就懂了，见截图：

算法字面解释如下：

第 1 行：这个过程用到的所有输入 - l 层的输出 Uj|i，路由迭代次数 r
第 2 行：定义 bij 是 l 层 VNi 应该连接 l+1 层 VNj 的可能性，初始值为 0
第 3 行：执行第 4-7 行 r 次
第 4 行：对 l 层的 VNi，将 bij 用 softmax 转化成概率 cij
第 5 行：对 l+1 层的 VNj，加权求和 sj
第 6 行：对 l+1 层的 VNj，压缩 sj 得到 vj
第 7 行：根据 Uj|i 和 vj 的关系来更新 bij
算法逻辑解释如下：

第 1 行无需说明，唯一要指出的是迭代次数为 3 次，Hinton 在他论文里这样说道
第 2 行初始化所有 b 为零，这是合理的。因为从第 4 行可看出，只有这样 c 才是均匀分布的，暗指“l 层 VN 到底要传送输出到 l+1 层哪个 VN 是最不确定的”
第 4 行的 softmax 函数产出是非负数而且总和为 1，致使 c 是一组概率变量
第 5 行的 sj 就是小节 2.3 第二步里面讲的红色簇心，可以认为是低层所有 VN 的“共识”输出
第 6 行的 squash 确保向量 sj 的方向不变，但长度不超过 1，因为长度代表 VN 具有给定特征的概率
第 7 行是动态路由的精华，用 Uj|i 和 vj 的点积 (dot product) 更新 bij，其中前者是 l 层 VNi对 l+1 层 VNj 的“个人”预测，而后者是所有 l 层 VN 对 l+1 层 VNj 的“共识”预测：
当两者相似，点积就大，bij 就变大，低层 VNi 连接高层 VNj 的可能性就变大
当两者相异，点积就小，bij 就变小，低层 VNi 连接高层 VNj 的可能性就变小
下面两幅图帮助进一步理解第 7 行的含义，第一幅讲的是点积，论文中用点积来度量两个向量的相似性，当然还有很多别的度量方式。

损失函数

由于 Capsule 允许多个分类同时存在，所以不能直接用传统的交叉熵 (cross-entropy) 损失，一种替代方案是用间隔损失 (margin loss)

其中，

• k 是分类
• Tk 是分类的指示函数 (k 类存在为 1，不存在为 0)
• m+ 为上界，惩罚假阳性 (false positive) ，即预测 k 类存在但真实不存在，识别出来但错了
• m- 为下界，惩罚假阴性 (false negative) ，即预测 k 类不存在但真实存在，没识别出来
• λ 是比例系数，调整两者比重

总的损失是各个样例损失之和。论文中 m+= 0.9, m-= 0.1, λ = 0.5，用大白话说就是

• 如果 k 类存在，||vk|| 不会小于 0.9
• 如果 k 类不存在，||vk|| 不会大于 0.1

惩罚假阳性的重要性大概是惩罚假阴性的重要性的 2 倍

胶囊网络推荐阅读

标题	说明	附加
《Dynamic Routing Between Capsules》	原始论文	2017
《胶囊间的动态路由》	论文翻译	AI研习社
cifar10_cnn_capsule	Keras 实现	2018
CapsNet-Tensorflow	TensorFlow实现	2018
胶囊网络到底是什么东东？		2018
如何理解和使用胶囊网络	应用	2019

Dynamic Routing Between Capsules

Sara Sabour, Nicholas Frosst, Geoffrey E Hinton
(Submitted on 26 Oct 2017 (v1), last revised 7 Nov 2017 (this version, v2))

A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or an object part. We use the length of the activity vector to represent the probability that the entity exists and its orientation to represent the instantiation parameters. Active capsules at one level make predictions, via transformation matrices, for the instantiation parameters of higher-level capsules. When multiple predictions agree, a higher level capsule becomes active. We show that a discrimininatively trained, multi-layer capsule system achieves state-of-the-art performance on MNIST and is considerably better than a convolutional net at recognizing highly overlapping digits. To achieve these results we use an iterative routing-by-agreement mechanism: A lower-level capsule prefers to send its output to higher level capsules whose activity vectors have a big scalar product with the prediction coming from the lower-level capsule.

Subjects: Computer Vision and Pattern Recognition (cs.CV)
Cite as: arXiv:1710.09829 [cs.CV]
(or arXiv:1710.09829v2 [cs.CV] for this version)

---

参考文献

[1] 王圣元‏.看完这篇，别说你还不懂Hinton大神的胶囊网络[DB/OL]. http://www.sohu.com/a/226611009_633698, 2018-08-24.