论文核心代码,TensorFlow 实现
1 | def selu(x): |
| 标题 | 说明 | 附加 |
|---|---|---|
| 《Self-Normalizing Neural Networks》 | 原始论文 | 2017 |
| 引爆机器学习圈:「自归一化神经网络」提出新型激活函数SELU | 翻译 | 2017 |
| 【文献阅读】Self-Normalizing Neural Networks | CSDN TensorSense | 2017 |
| 如何评价 Self-Normalizing Neural Networks 这篇论文? | 知乎评价 | |
| Compare SELUs (scaled exponential linear units) with other activations on MNIST, CIFAR10, etc. | SELU 在不同数据集实验 | 2017 |
Self-Normalizing Neural Networks
Günter Klambauer, Thomas Unterthiner, Andreas Mayr, Sepp Hochreiter
(Submitted on 8 Jun 2017 (v1), last revised 7 Sep 2017 (this version, v5))
Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via recurrent neural networks (RNNs). However, success stories of Deep Learning with standard feed-forward neural networks (FNNs) are rare. FNNs that perform well are typically shallow and, therefore cannot exploit many levels of abstract representations. We introduce self-normalizing neural networks (SNNs) to enable high-level abstract representations. While batch normalization requires explicit normalization, neuron activations of SNNs automatically converge towards zero mean and unit variance. The activation function of SNNs are “scaled exponential linear units” (SELUs), which induce self-normalizing properties. Using the Banach fixed-point theorem, we prove that activations close to zero mean and unit variance that are propagated through many network layers will converge towards zero mean and unit variance — even under the presence of noise and perturbations. This convergence property of SNNs allows to (1) train deep networks with many layers, (2) employ strong regularization, and (3) to make learning highly robust. Furthermore, for activations not close to unit variance, we prove an upper and lower bound on the variance, thus, vanishing and exploding gradients are impossible. We compared SNNs on (a) 121 tasks from the UCI machine learning repository, on (b) drug discovery benchmarks, and on (c) astronomy tasks with standard FNNs and other machine learning methods such as random forests and support vector machines. SNNs significantly outperformed all competing FNN methods at 121 UCI tasks, outperformed all competing methods at the Tox21 dataset, and set a new record at an astronomy data set. The winning SNN architectures are often very deep. Implementations are available at: github.com/bioinf-jku/SNNs.
深度学习不仅通过卷积神经网络(CNN)变革了计算机视觉,同时还通过循环神经网络(RNN)变革了自然语言处理。然而,带有标准前馈神经网络(FNN)的深度学习很少有成功的案例。通常表现良好的 FNN 都只是浅层模型,因此不能挖掘多层的抽象表征。所以我们希望引入自归一化神经网络(self-normalizing neural networks/SNNs)以帮助挖掘高层次的抽象表征。虽然批归一化要求精确的归一化,但 SNN 的神经元激励值可以自动地收敛到零均值和单位方差。SNN 的激活函数即称之为「可缩放指数型线性单元(scaled exponential linear units/SELUs)」,该单元引入了自归一化的属性。使用 Banach 的不动点定理(fixed-point theorem),我们证明了激励值逼近于零均值和单位方差并且通过许多层的前向传播还是将收敛到零均值和单位方差,即使是存在噪声和扰动的情况下也是这样。这种 SNN 收敛属性就允许 (1) 训练许多层的深度神经网络,同时 (2) 采用强正则化、(3) 令学习更具鲁棒性。此外,对于不逼近单位方差的激励值,我们证明了其方差存在上确界和下确界,因此梯度消失和梯度爆炸是不可能出现的。同时我们采取了 (a) 来自 UCI 机器学习库的 121 个任务,并比较了其在 (b) 新药发现基准和 (c) 天文学任务上采用标准 FNN 和其他机器学习方法(如随机森林、支持向量机等)的性能。SNN 在 121 个 UCI 任务上显著地优于所有竞争的 FNN 方法,并在 Tox21 数据集上超过了所有的竞争方法,同时 SNN 还在天文数据集上达到了新纪录。该实现的 SNN 架构通常比较深,实现可以在以下链接获得:http://github.com/bioinf-jku/SNNs。
Comments: 9 pages (+ 93 pages appendix)
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)
Journal reference: Advances in Neural Information Processing Systems 30 (NIPS 2017)
Cite as: arXiv:1706.02515 [cs.LG]
(or arXiv:1706.02515v5 [cs.LG] for this version)
实验结论
我们提出了自归一化神经网络,并且已经证明了当神经元激励在网络中传播时是在朝零均值(zero mean)和单位方差(unit variance)的趋势发展的。而且,对于没有接近单位方差的激励,我们也证明了方差映射的上线和下限。于是 SNN 不会产梯度消失和梯度爆炸的问题。因此,SNN 非常适用于多层的结构,这使我们可以引入一个全新的正则化(regularization)机制,从而更稳健地进行学习。在 121UCI 基准数据集中,SNN 已经超过了其他一些包括或不包括归一化方法的 FNN,比如批归一化(batch)、层级归一化(layer)、权值归一化(weight normalization)或其它特殊结构(Highway network 或 Residual network)。SNN 也在药物研发和天文学任务中产生了完美的结果。和其他的 FNN 网络相比,高性能的 SNN 结构通常深度更深。
基于 SELUs 的模型的论文
Models and architectures built on Self-Normalizing Networks
实验验证 SELU 的真实效果
MNIST-MLP-SELU VS MNIST-MLP-RELU
模型结构
MNIST_Conv_SELU
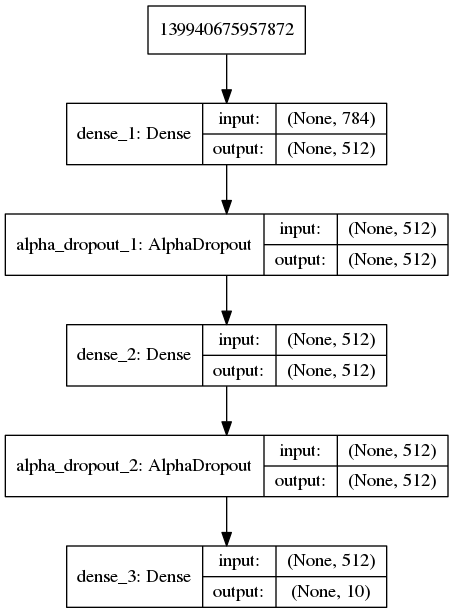
MNIST_Conv_RELU
实验结果
蓝色的线代表 SELU ,橙色的线代表 RELU。

结果分析
在 MNIST 数据集,多层前馈神经网络模型条件下,SELU 在训练集的效果差于 RELU,但是 SELU 在验证集效果与 RELU 几乎一致,且 SELU 训练时间更长。
MNIST-Conv-SELU VS MNIST-Conv-RELU
模型结构
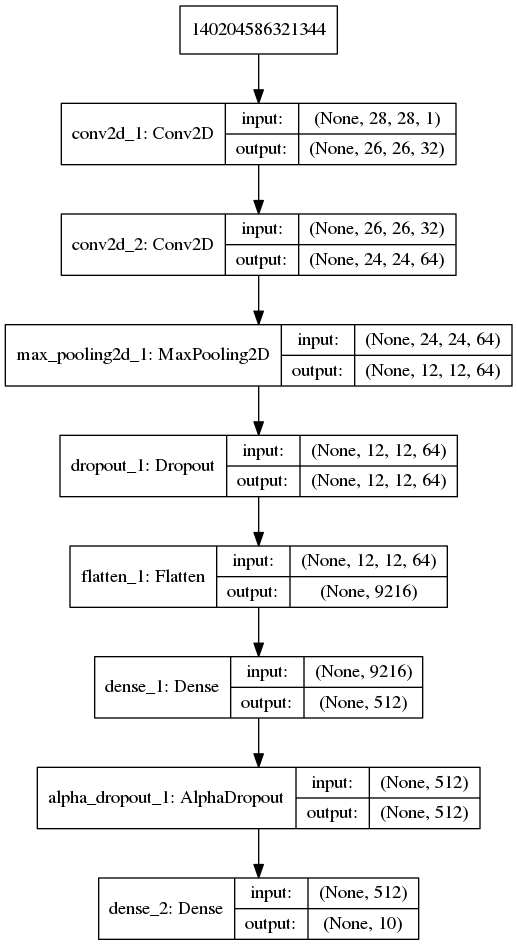
MNIST_Conv_SELU

MNIST_Conv_RELU

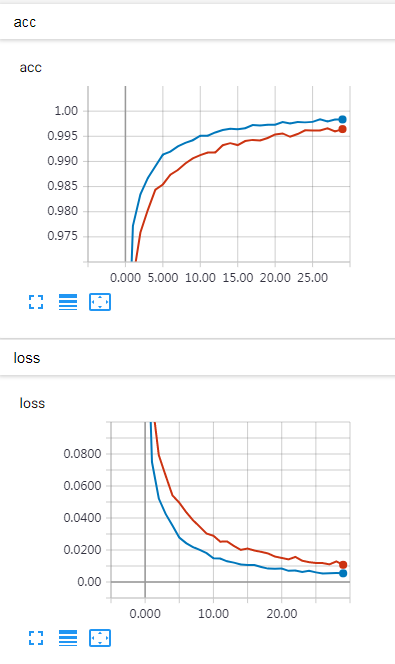
实验结果
蓝色的线代表 SELU ,橙色的线代表 RELU


结果分析
在 MNIST 数据集,多层卷积神经网络模型条件下,SELU 在训练集的效果优于 RELU,但是 SELU 在验证集效果差于 RELU ,且 SELU 训练时间更长。
CIFAR10_Conv_SELU VS CIFAR10_Conv_RELU
模型结构
CIFAR10_Conv_SELU
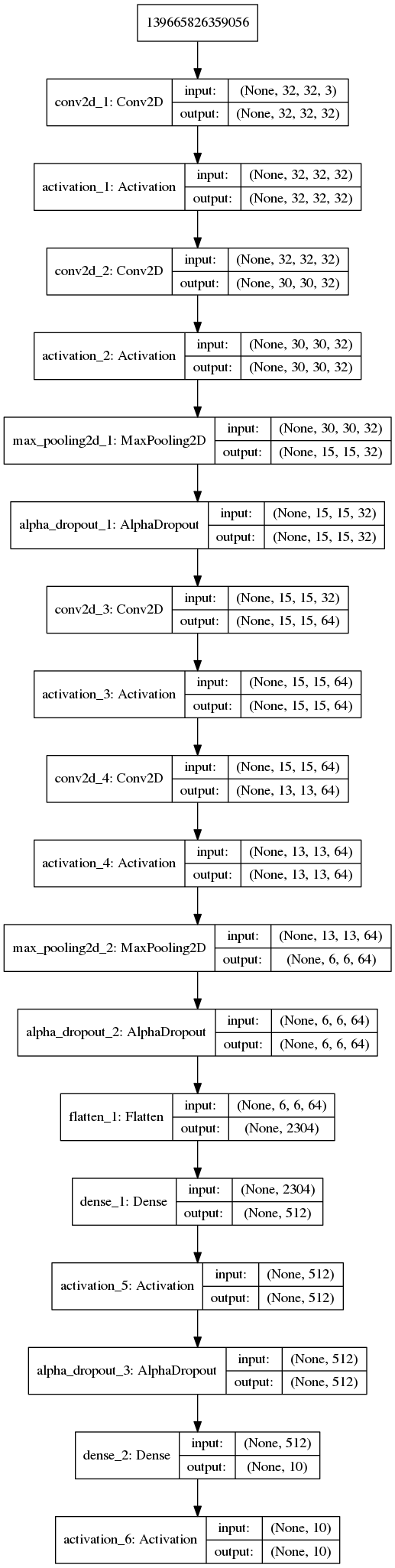
CIFAR10_Conv_RELU

实验结果
灰色线代表 SELU,绿色线代表 RELU。
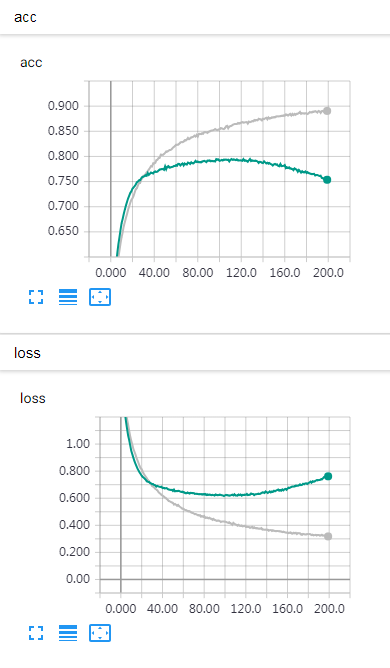
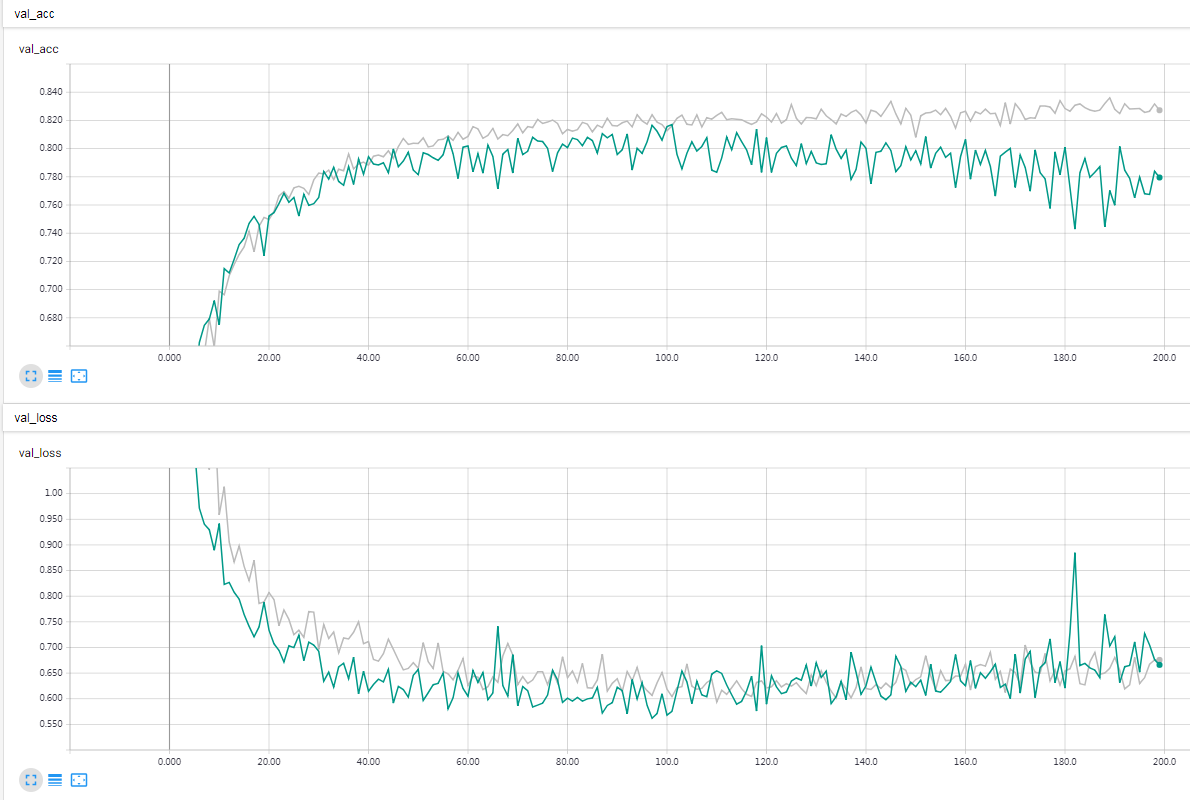
结果分析
在 CIFAR10 数据集,多层卷积神经网络模型条件下,SELU 在训练集的效果优于 RELU,但是 SELU 在验证集效果与 RELU 一致,且 RELU 更不易发生过拟合,SELU 训练时间更长。
reuters_mlp_relu_vs_selu
模型结构
reuters_mlp_selu

reuters_mlp_relu

实验结果
灰色的线代表 SELU,绿色的线代表 RELU。

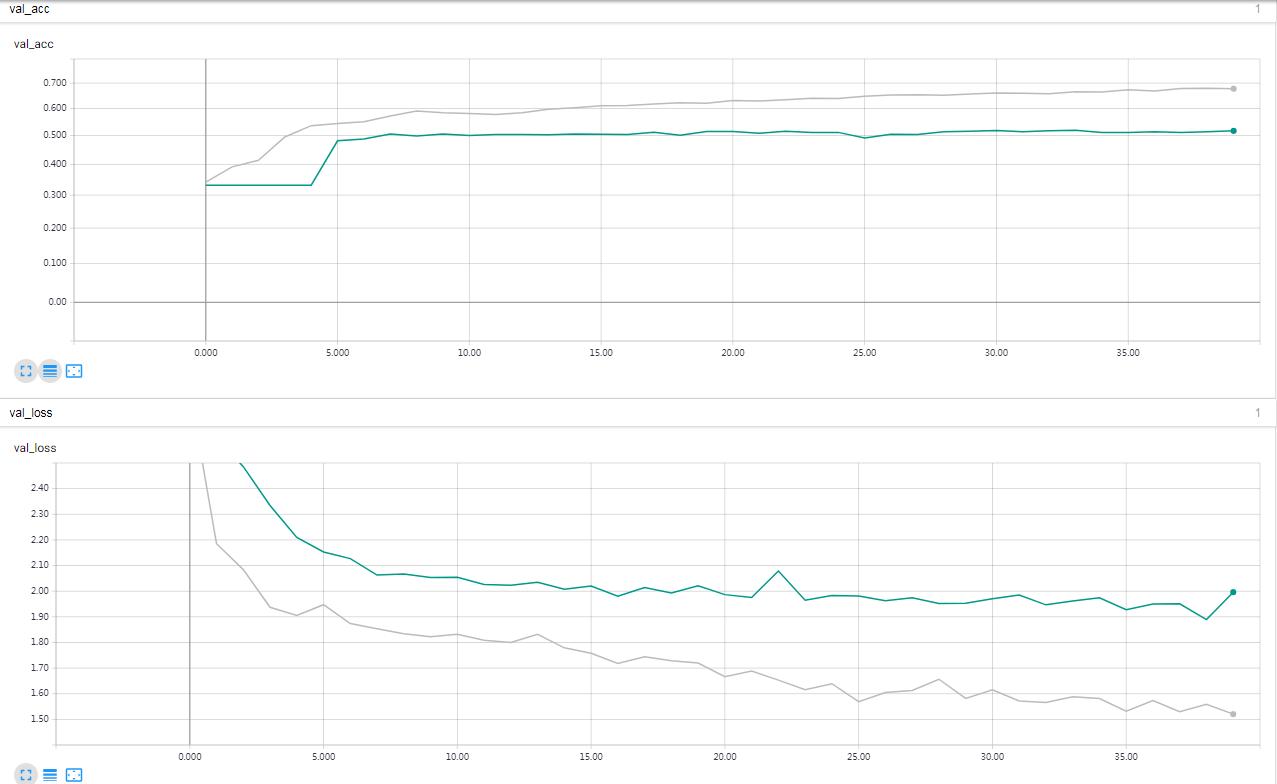
结果分析
在 reuters 数据集,多层前馈神经网络模型条件下,SELU 在训练集的效果差于 RELU,但是 SELU 在验证集效果稍稍优于 RELU ,但 SELU 训练时间更长。
本文结论
SELU 只有在特殊限定的数据集和网络模型结构的条件下会优于 RELU,一般情况下 RELU 训练速度更快,且更不容易发生过拟合。所以根据现有证据,SELU 比 RELU 没有显著优势,一般情况下选择 RELU 更优。

