感受视野

在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。通俗点的解释是，特征图上的一个点对应输入图上的区域，如下图所示。

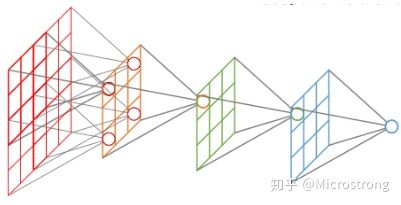
感受野计算时有下面几个知识点需要知道：

最后一层（卷积层或池化层）输出特征图感受野的大小等于卷积核的大小。
第i层卷积层的感受野大小和第i层的卷积核大小和步长有关系，同时也与第（i+1）层感受野大小有关。
计算感受野的大小时忽略了图像边缘的影响，即不考虑padding的大小。

关于感受野大小的计算方式是采用从最后一层往下计算的方法，即先计算最深层在前一层上的感受野，然后逐层传递到第一层，使用的公式可以表示如下：

$RF_i=(RF_{i+1} - 1) \times stride_i + Ksize$

其中,$RF_i$和$RF_{i+1}$分别是是第i层和第i+1层卷积层的感受视野，stride是卷积的步长，Ksize是本层卷积核的大小。

注意，由于没有考虑padding的影响，最终算出的感受视野可能会大于原图。

感受视野例题

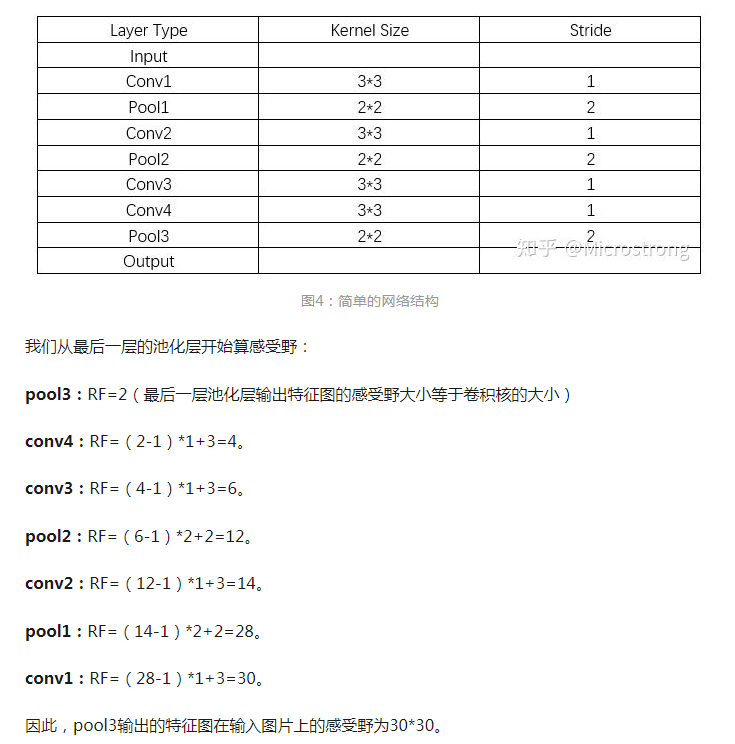
理解原理

卷积神经网络中感受野的理解和计算

维度变化

conv2d的卷积操作后维度变化

输入维度：$W_1 \times H_1 \times D_1$，分别代表输入样本的长宽高

卷积操作的超参数

卷积核个数：$K$
卷积核大小：$F \times F$
滑动步长（Stride）：$S$
填充（Padding）：$P$

则输出的维度为$W_2 \times H_2 \times D_2$，其中

$W_2=\lceil (W_1 - F + 2P)/S \rceil + 1$
$H_2=\lceil (W_1 - F + 2P)/S \rceil + 1$
$D_2=K$

由于CNN的参数共享机制，每个卷积核的参数个数为$F \times F \times D_1$，共有$(F \times F \times D_1) \times K$个权重和$K$个偏置。

若想要卷积后得到的矩阵长宽与卷积前保持一致，则当$S=1$时

卷积核为3时 padding 选择1
卷积核为5时 padding 选择2
卷积核为7时 padding 选择3

例题

100×100×3，3×3 卷积核，输出是 50×50×10，算进行了多少次乘-加操作？

卷积运算次数 = 输出元素个数 x 输入通道数= 50×50×10x3 = 75000
乘法运算次数 = 卷积运算次数 x 卷积和元素个数 = 75000 x 3 x 3
加法运算次数 = 卷积运算次数 x (卷积核元素个数 + 偏置个数 - 1) = 75000 x ( 3 x 3 + 1 - 1) = 225000

conv2d的卷积操作后维度变化（”VALID” or “SAME”）

注意，在使用神经网络框架时常常会使用padding这个参数，计算方式会有所不同。

1	padding: A string, either "VALID" or "SAME". The padding algorithm.

Valid: 用过滤器在输入的矩阵中按步长移动时候，会把最后的不足部分的列和行抛弃；
Same: 先在输入矩阵上下各加个值为0的行，在左右各加个个值为0的列，也就是用0把原先的矩阵包裹一层，然后在移动的时候如果输入矩阵的列或者行长度不够，就用0来补齐

计算方法

SAME:

out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2]))

VALID:

out_height = ceil(float(in_height - filter_height + 1) / float(strides1))
out_width = ceil(float(in_width - filter_width + 1) / float(strides[2]))

例题

max_pool2d的池化操作后维度变化

输入维度：$W_1 \times H_1 \times D_1$，分别代表输入样本的长宽高

池化操作的超参数

池化层大小：$F \times F$
滑动步长（Stride）：$S$
填充（Padding）：$P$

则输出的维度为$W_2 \times H_2 \times D_2$，其中

$W_2=\lceil (W_1 - F + 2P)/S \rceil + 1$
$H_2=\lceil (W_1 - F + 2P)/S \rceil + 1$
$D_2=D_1$

神经网络的参数量计算方法

Embedding

Neural network structure	Parameter quantity
input_shape [batch_size, input_length]
Dense(input_dim, output_dim)	input_dim * output_dim
output_shape [batch_size, input_length, output_dim]

Dense

Neural network structure	Parameter quantity
input_shape [batch_size, input_dim]
Dense(units)	input_dim * units + units
output_shape [batch_size, units]

Conv2D

Neural network structure	Parameter quantity
input_shape [batch_size, rows, cols, input_dim]
Conv2D(filters, kernel_size)	kernel_size kernel_size filters + filters
output_shape [batch_size, new_rows, new_cols, filters]

LSTM

h_depth = self._num_units if self._num_proj is None else self._num_proj

self._kernel = self.add_variable(
    _WEIGHTS_VARIABLE_NAME,
    shape=[input_depth + h_depth, 4 * self._num_units])
self._bias = self.add_variable(
    _BIAS_VARIABLE_NAME,
    shape=[4 * self._num_units],
    initializer=init_ops.zeros_initializer(dtype=self.dtype))

Neural network structure	Parameter quantity
input_shape [batch_size, input_length, input_depth]
LSTM(num_units)	(input_depth + num_units) (4 num_units) + 4 * num_units
output_shape [batch_size, input_length, num_units]

人工智能

深度学习中的计算题